Mathematics
In figure (1) given below, ABCD is a parallelogram. Points P and Q on BC trisect BC into three equal parts. Prove that : area of ∆APQ = area of ∆DPQ = (area of ||gm ABCD)
Related Questions
In figure (2) given below, area of ∆ABD is 24 sq. units. If AB = 8 units, find the height of △ABC.

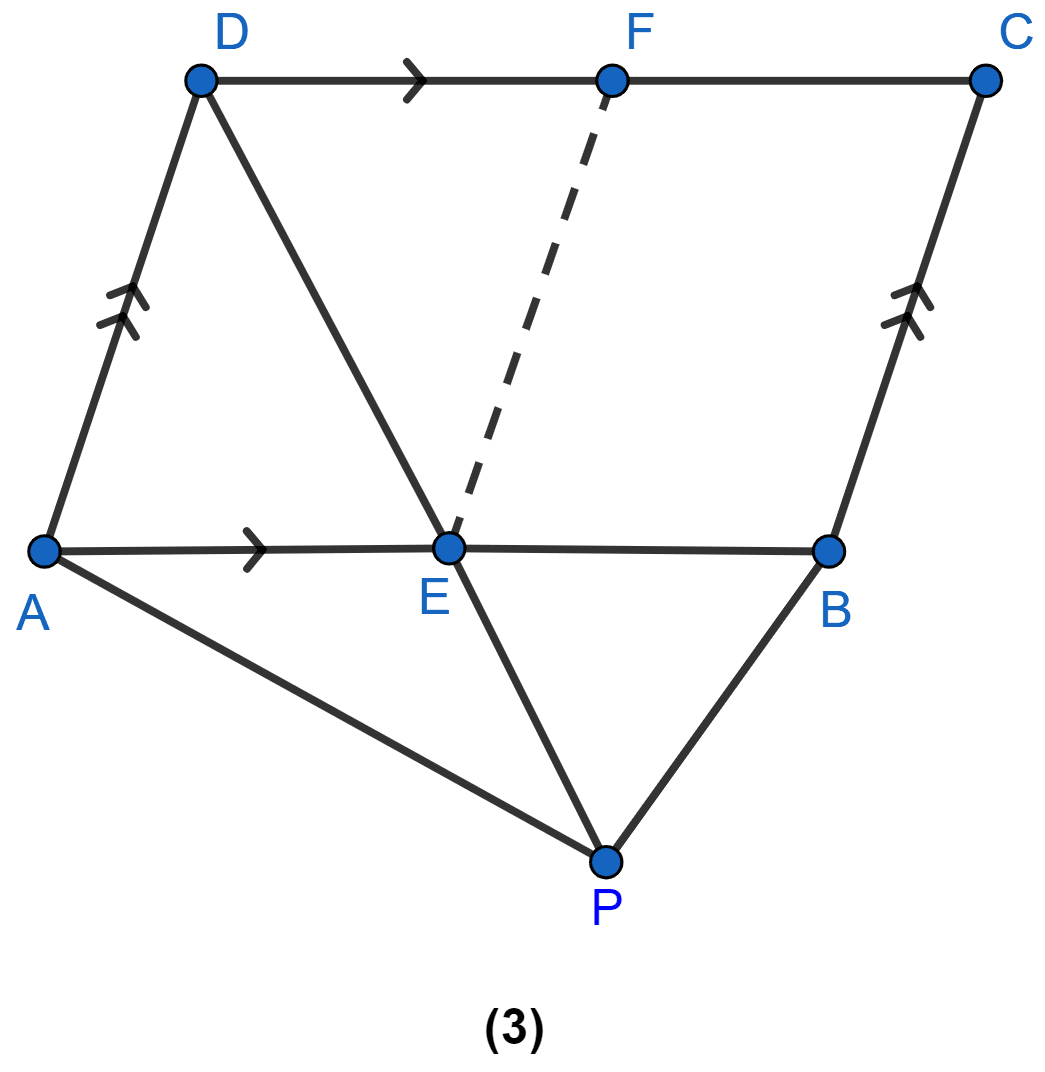
In figure (3) given below, E and F are midpoints of sides AB and CD, respectively, of parallelogram ABCD. If the area of parallelogram ABCD is 36 cm2,
(i) state the area of ∆APD.
(ii) Name the parallelogram whose area is equal to the area of ∆APD.
In figure (2) given below, DE is drawn parallel to the diagonal AC of the quadrilateral ABCD to meet BC produced at point E. Prove that area of quad. ABCD = area of ∆ABE.

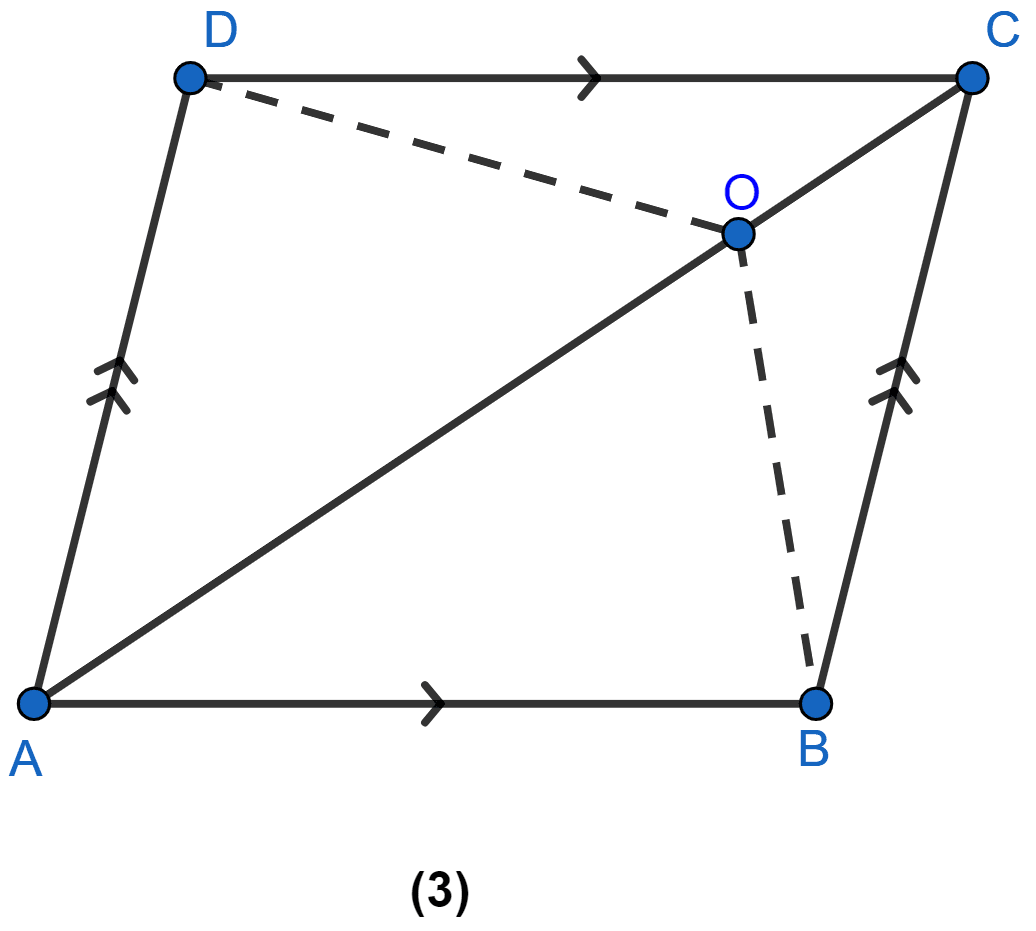
In the figure (3) given below, ABCD is a parallelogram. O is any point on the diagonal AC of the parallelogram. Show that the area of ∆AOB is equal to the area of ∆AOD.