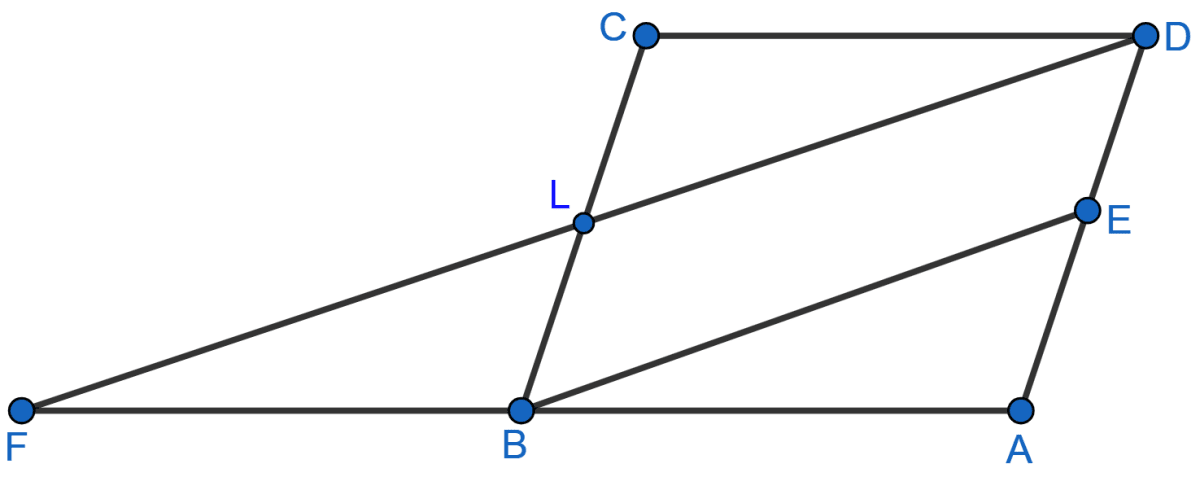
In △ABC, D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F. Prove that BDEF is a parallelogram. If AB = 8 cm and BC = 9 cm, find the perimeter of the parallelogram BDEF.

Since, D and E are mid-points of AB and AC respectively,

DE || BC or DE || BF and DE = $\dfrac{1}{2}$BC ……(By midpoint theorem) …..(i)

Given, through E, a straight line is drawn parallel to AB to meet BC at F.

F will be mid-point of BC (By converse of mid-point theorem).

Since, F is midpoint of BC,

∴ BF = $\dfrac{1}{2}$BC …..(ii)

From (i) and (ii) we get,

DE = BF and DE || BF.

Since, F and E are mid-points of BC and AC respectively,

FE || AB or FE || BD and FE = $\dfrac{1}{2}$AB ……(By midpoint theorem) …..(iii)

Since, D is midpoint of AB,

∴ BD = $\dfrac{1}{2}$AB …..(iv)

From (iii) and (iv) we get,

BD = FE and BD || FE.

Since, DE = BF, DE || BF and BD = FE, BD || FE

Hence, proved that BDEF is a parallelogram.

Perimeter of BDEF = BD + DE + FE + BF = BD + DE + BD + FE = 2(BD + FE).

BD = $\dfrac{1}{2}$AB = $\dfrac{1}{2}(8)$ = 4 cm.

FE = $\dfrac{1}{2}$BC = $\dfrac{1}{2}(9)$ = 4.5 cm.

Perimeter of BDEF = 2(BD + FE) = 2(4 + 4.5) = 2 × 8.5 = 17 cm.

Hence, perimeter of BDEF = 17 cm.