Mathematics
If D, E and F are mid-points of the sides BC, CA and AB respectively of a △ABC, prove that AD and FE bisect each other.
Mid-point Theorem
18 Likes
Answer
△ABC with D, E and F as mid-points of the sides BC, CA and AB is shown below:
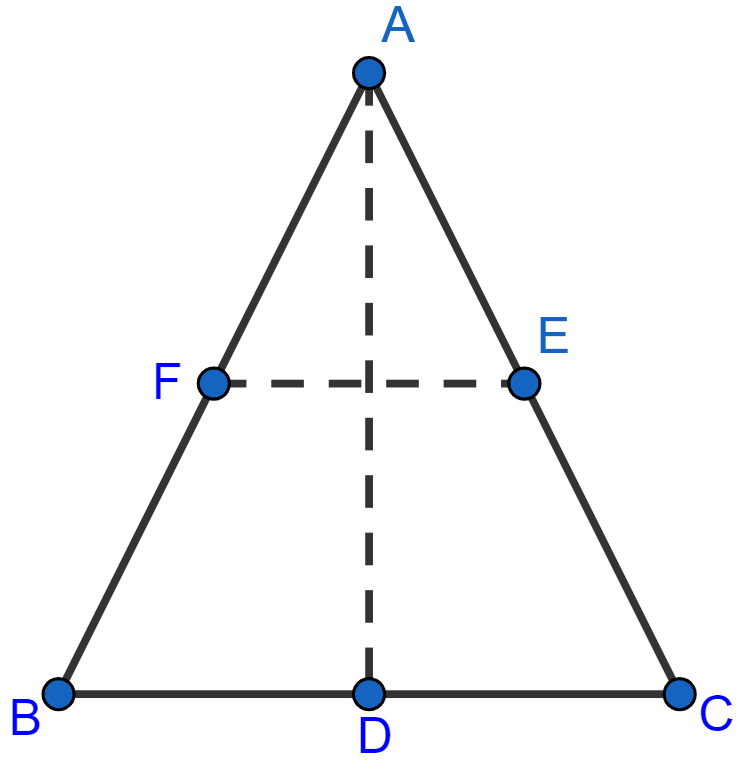
D and E are midpoints of BC and CA respectively,
DE = AB and DE || AB or DE || AF …….(1)
Since,
F is midpoint of AB,
AF = AB
∴ AF = DE …….(2)
F and D are midpoints of AB and BC respectively,
FD = AC and FD || AC or FD || AE …….(3)
Since,
E is midpoint of AC,
AE = AC
∴ FD = AE …….(4)
From 1, 2, 3 and 4 we get,
DE || AF, AF = DE and FD || AE, FD = AE.
Hence, AEDF is a parallelogram.
∴ AD and EF bisect each other.
Hence, AD and EF bisect each other.
Answered By
12 Likes
Related Questions
ABCD is a rhombus with P, Q and R as mid-points of AB, BC and CD respectively. Prove that PQ ⊥ QR.
The diagonals of a quadrilateral ABCD are perpendicular. Show that the quadrilateral formed by joining the mid-points of its adjacent sides is a rectangle.
In △ABC, D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F. Prove that BDEF is a parallelogram. If AB = 8 cm and BC = 9 cm, find the perimeter of the parallelogram BDEF.
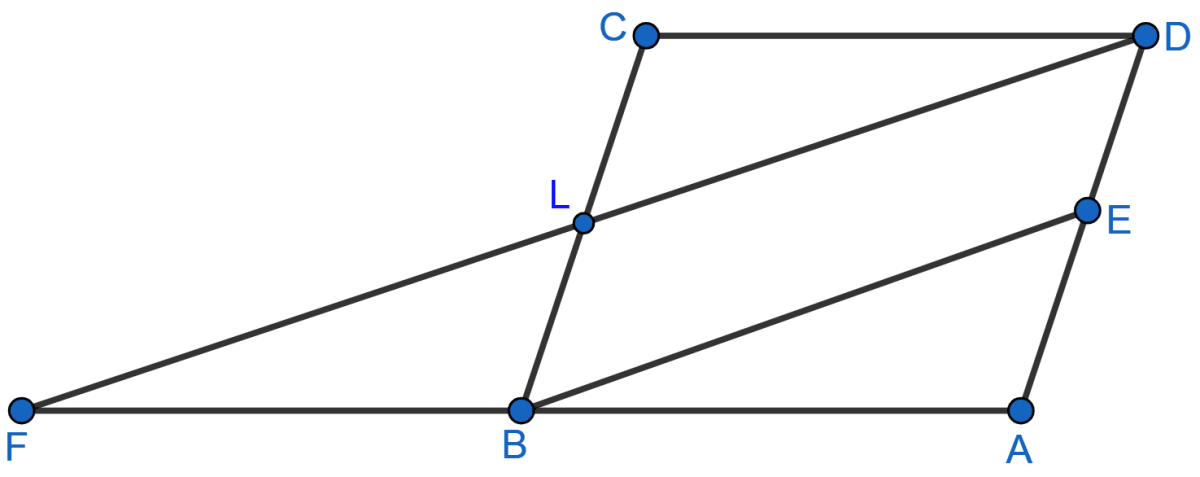
In the adjoining figure, ABCD is a parallelogram and E is mid-point of AD. DL || EB meets AB produced at F. Prove that B is mid-point of AF and EB = LF.