Mathematics
In the adjoining figure, ABCD is a parallelogram and E is mid-point of AD. DL || EB meets AB produced at F. Prove that B is mid-point of AF and EB = LF.
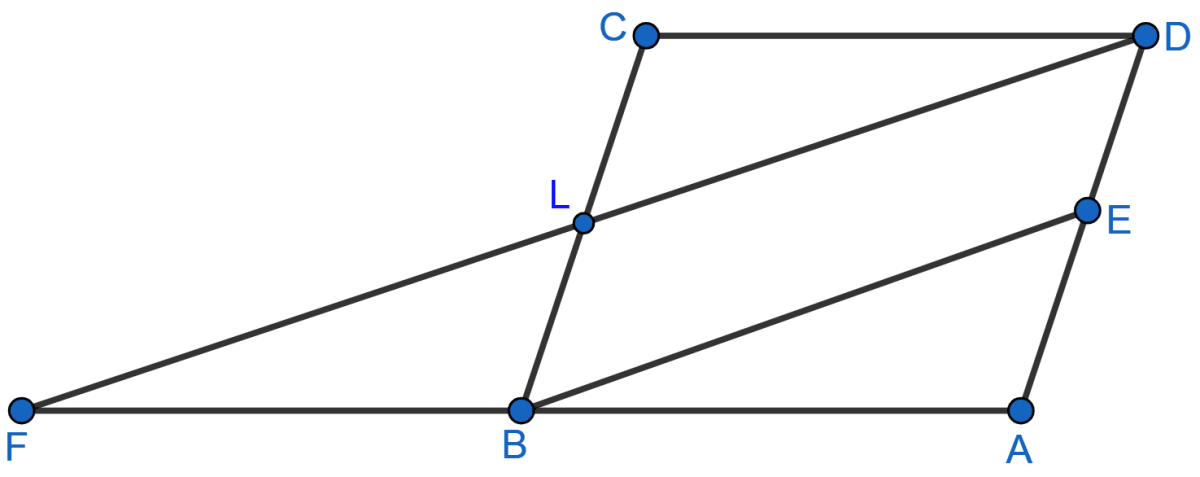
Mid-point Theorem
18 Likes
Answer
Given, DL || EB.
Since, DL || BE we can say that,
⇒ BE || DF
In △AFD,
E is midpoint of AD and BE is parallel to DF,
∴ B is midpoint of AF (By converse of midpoint theorem).
In BEDL,
LD || BE and BL || DE
∴ BEDL is a parallelogram.
Since, BEDL is a parallelogram opposite sides are equal.
Let LD = BE = x.
E is midpoint of AD and B is the midpoint of AF
By midpoint theorem,
BE = FD
FD = 2BE = 2x.
LF = FD - LD = 2x - x = x.
Since, LF = BE = x.
Hence, proved that B is midpoint of AF and EB = LF.
Answered By
9 Likes
Related Questions
If D, E and F are mid-points of the sides BC, CA and AB respectively of a △ABC, prove that AD and FE bisect each other.
In △ABC, D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F. Prove that BDEF is a parallelogram. If AB = 8 cm and BC = 9 cm, find the perimeter of the parallelogram BDEF.
The diagonals of a quadrilateral ABCD are perpendicular. Show that the quadrilateral formed by joining the mid-points of its adjacent sides is a rectangle.
In the adjoining figure, ABCD is a parallelogram. If P and Q are mid-points of sides CD and BC respectively. Show that CR = AC.
