Mathematics
In △ABC, AP : PB = 2 : 3. PO is parallel to BC and is extended to Q so that CQ is parallel to BA. Find :
(i) area △APO : area △ABC
(ii) area △APO : area △CQO.

Similarity
Answer
(i) Given,
Considering △APO and △ABC,
∠ A = ∠ A (Common angles)
∠ APO = ∠ ABC (Corresponding angles are equal)
Hence, by AA axiom △APO ~ △ABC.
We know that, the ratio of the areas of two similar triangles is equal to the ratio of the square of their corresponding sides.
Hence, the ratio of the area of △APO : area of △ABC = 4 : 25.
(ii) In parallelogram PBCQ opposite sides are equal,
so, PB = QC. Hence, .
Considering △APO and △CQO,
∠ AOP = ∠ QOC (Vertically opposite angles)
∠ OAP = ∠ OCQ (Alternate angles are equal)
Hence, by AA axiom △APO ~ △CQO.
We know that, the ratio of the areas of two similar triangles is equal to the ratio of the square of their corresponding sides.
Hence, the ratio of the area of △APO : area of △CQO = 4 : 9.
Answered By
Related Questions
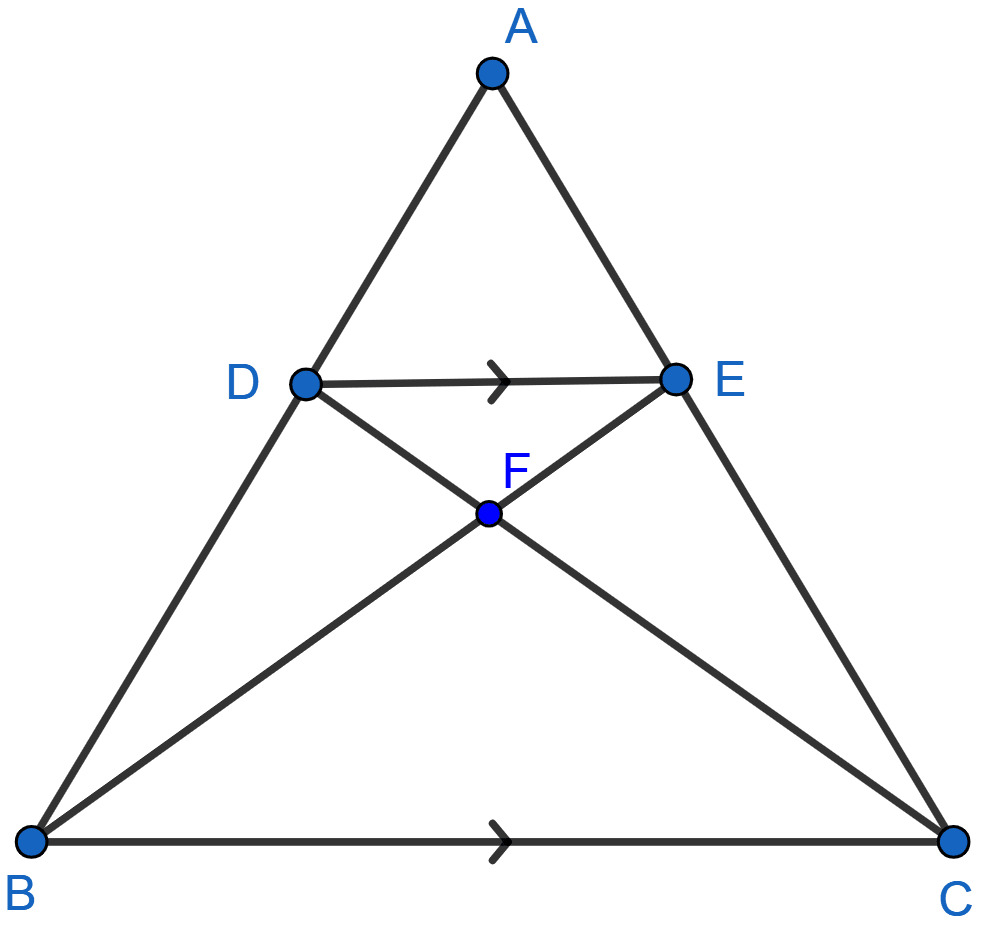
In the adjoining figure, ABC is a triangle. DE is parallel to BC and
(i) Determine the ratio
(ii) Prove that △DEF is similar to △CBF. Hence, find
(iii) What is the ratio of the areas of △DEF and △CBF ?
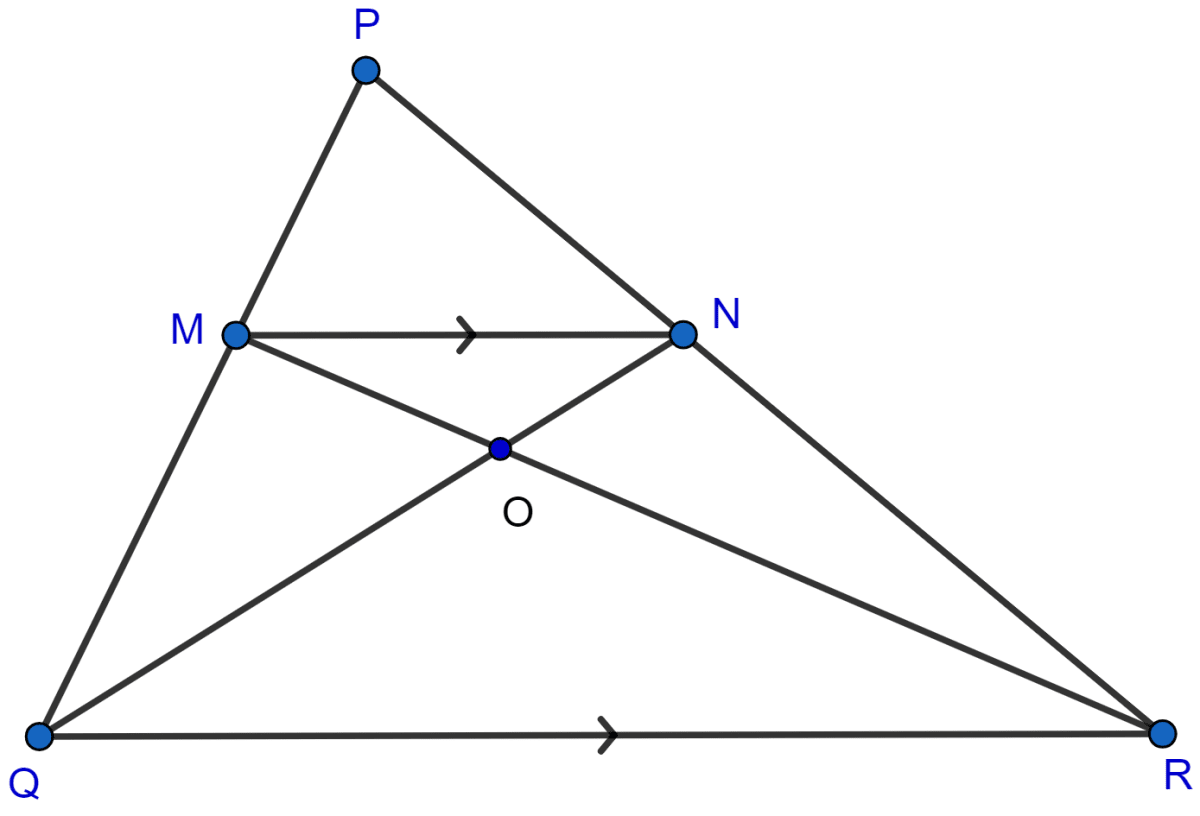
In △PQR, MN is parallel to QR and
(i) Find .
(ii) Prove that △OMN and △ORQ are similar.
(iii) Find area of △OMN : area of △ORQ.
In the figure (i) given below, ABCD is a trapezium in which AB || DC and AB = 2 CD. Determine the ratio of the areas of △AOB and △COD.

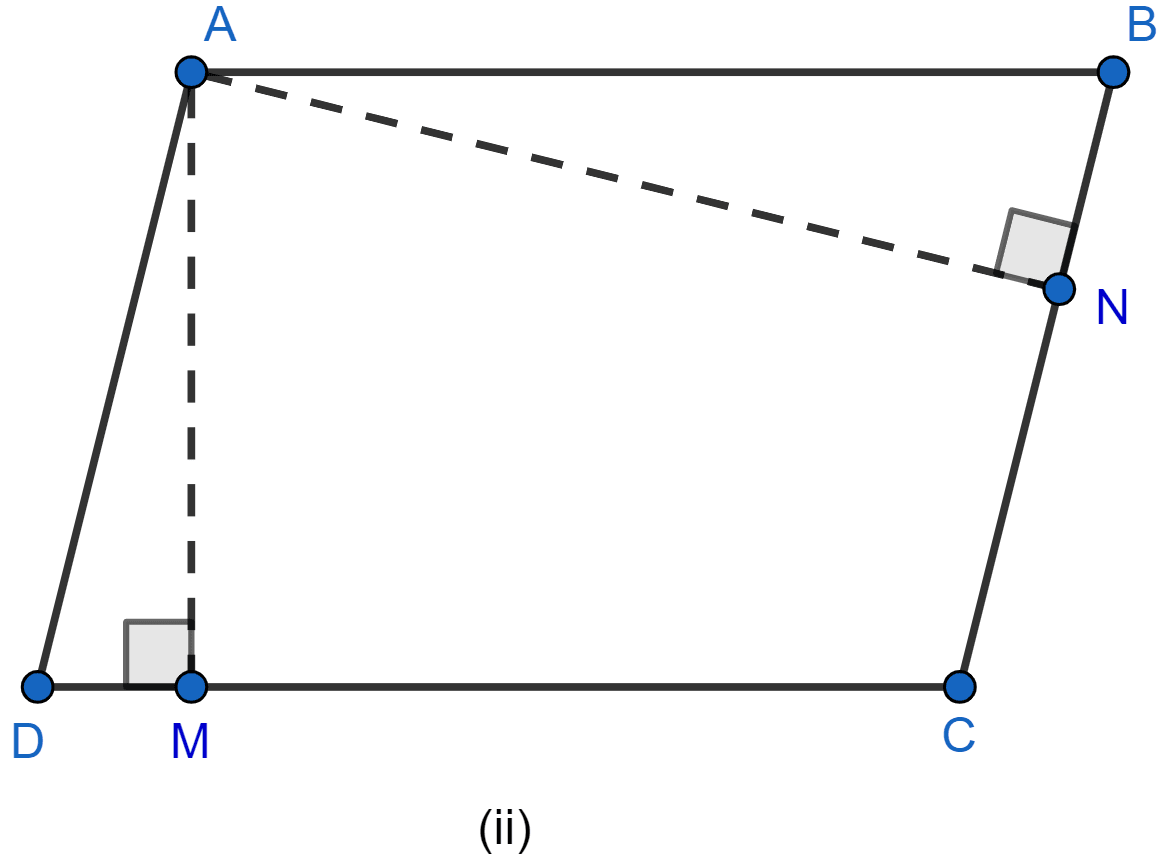
In the figure (ii) given below, ABCD is a parallelogram. AM ⊥ DC and AN ⊥ CB. If AM = 6 cm, AN = 10 cm and the area of parallelogram ABCD is 45 cm2, find
(i) AB
(ii) BC
(iii) area of △ADM : area of △ANB.