If the perimeter of a right angled triangle is 60 cm and its hypotenuse is 25 cm, find its area.

Let △ABC be the right angle triangle.

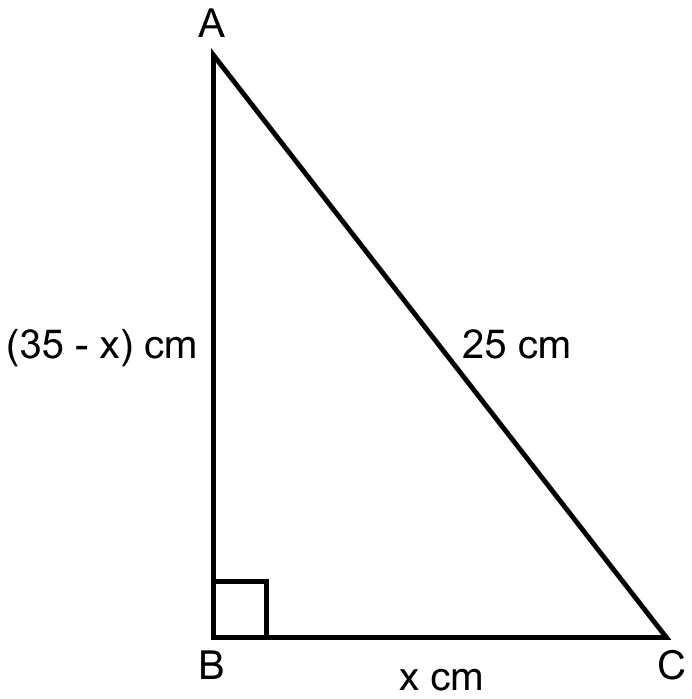
We know that,

Perimeter of a right-angled triangle = 60 cm

Hypotenuse = 25 cm

So, the sum of other two sides of triangle = 60 – 25 = 35 cm

Let base (BC) = x cm

So, AB = (35 - x) cm

Using the Pythagoras theorem,

⇒ AC² = AB² + BC²

⇒ 25² = (35 - x)² + x²

⇒ 625 = 1225 + x² - 70x + x²

⇒ 2x² - 70x + 600 = 0

Dividing by 2 on both sides,

⇒ x² - 35x + 300 = 0

⇒ x² - 15x - 20x + 300 = 0

⇒ x(x – 15) - 20(x - 15) = 0

⇒ (x - 15)(x - 20) = 0

⇒ x - 15 = 0 or x - 20 = 0

⇒ x = 15 or x = 20.

If x = 15, then 35 - x = 35 - 15 = 20 cm.

If x = 20, then 35 - x = 35 - 20 = 15 cm.

So, length of other two sides apart from hypotenuse are 15 cm and 20 cm.

Area = $\dfrac{1}{2}$ × base × height

Substituting the values we get,

A = $\dfrac{1}{2}$ × 15 × 20 = 150 cm².

Hence, area of triangle = 150 cm².