Mathematics
If the lines y = 3x + 7 and 2y + px = 3 are perpendicular to each other, find the value of p.
Straight Line Eq
4 Likes
Answer
Given lines,
⇒ y = 3x + 7 and 2y + px = 3
⇒ y = 3x + 7 and 2y = -px + 3
⇒ y = 3x + 7 and
Comparing above equations with y = mx + c we get,
Slope of 1st line = 3
Slope of 2nd line =
Since,
Product of slopes of perpendicular lines = -1.
Hence, p = .
Answered By
2 Likes
Related Questions
In the given figure, line AB meets y-axis at point A. Line through C(2, 10) and D intersects line AB at right angle at point P. Find :
(i) equation of line AB.
(ii) equation of line CD.
(iii) co-ordinates of point E and D.

Find the equation of the line through the points A(-1, 3) and B(0, 2). Hence, show that the points A, B and C(1, 1) are collinear.
In the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
(i) Write the co-ordinates of A.
(ii) Find the length of AB and AC.
(iii) Find the ratio in which Q divides AC.
(iv) Find the equation of the line AC.
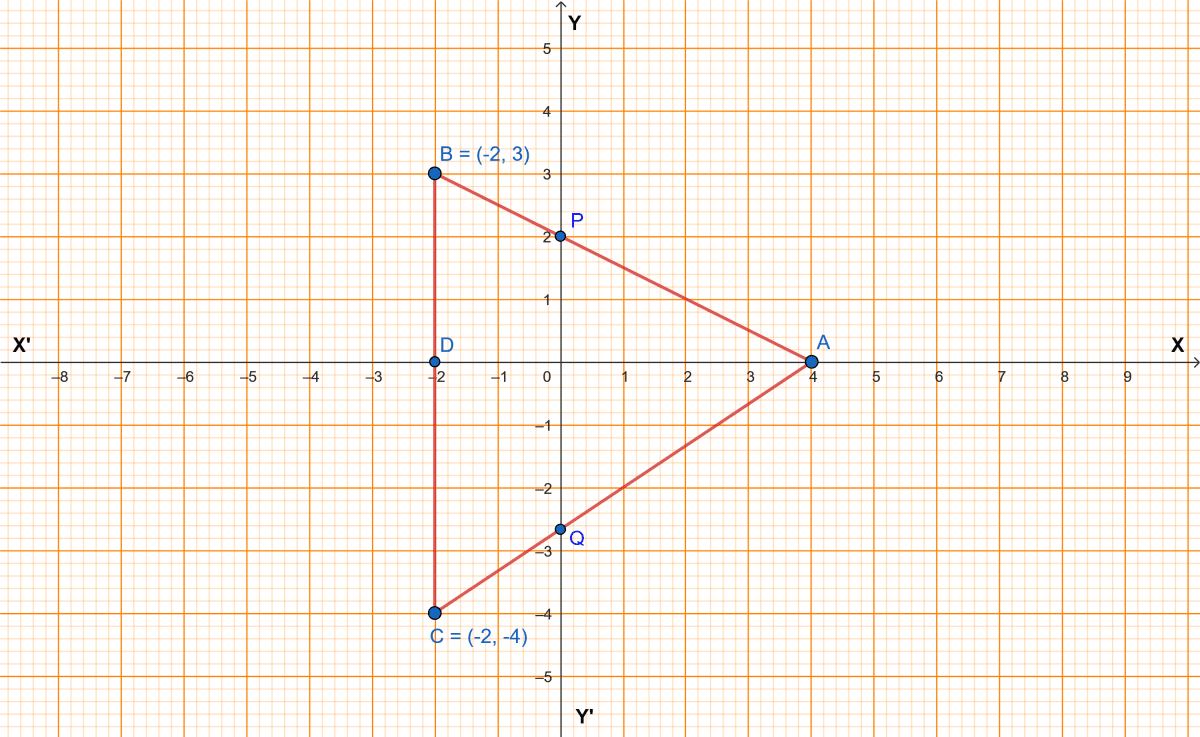
A line AB meets X-axis at A and Y-axis at B. P(4, -1) divides AB in the ratio 1 : 2.
(i) Find the co-ordinates of A and B.
(ii) Find the equation of the line through P and perpendicular to AB.
