Mathematics
If the length of each side of a rhombus is 8 cm and its one angle is 60°, then find the lengths of the diagonals of the rhombus.
Trigonometrical Ratios
41 Likes
Answer
We know that the diagonals of a rhombus bisect the opposite angles and are perpendicular to each other.
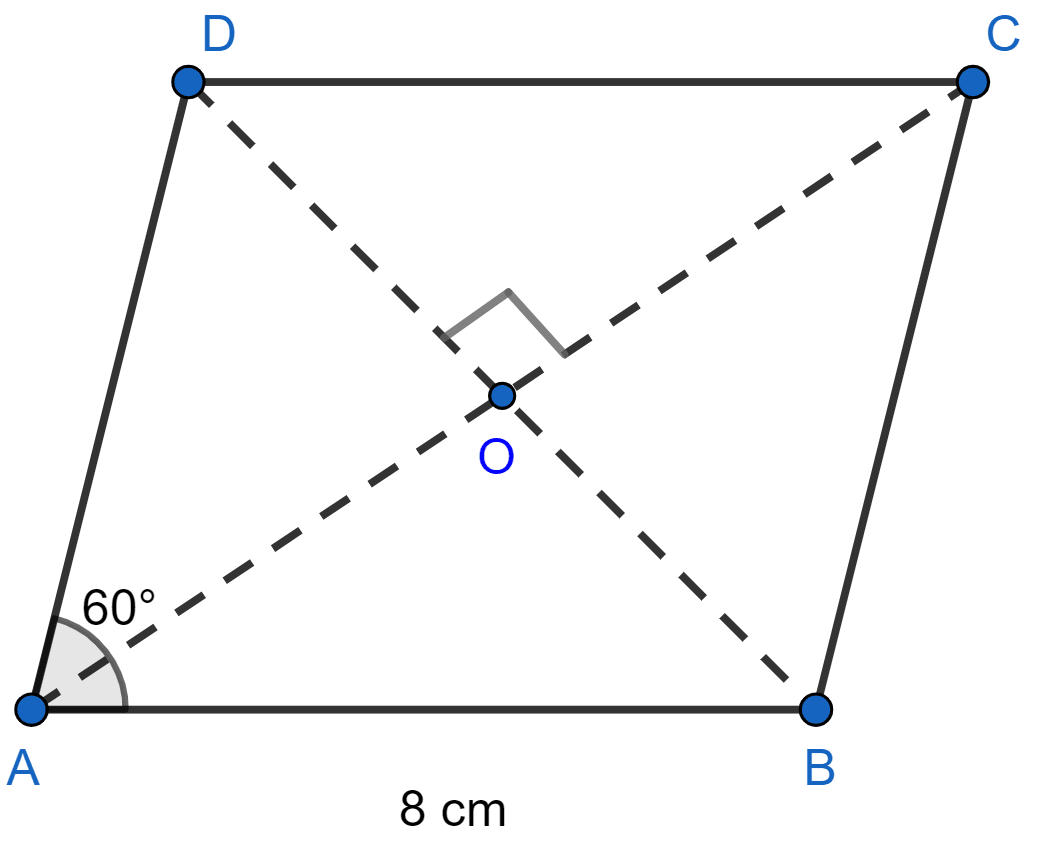
∴ ∠OAB = = 30°.
In right ∠AOB,
⇒ sin 30° =
⇒
⇒ OB =
⇒ OB = = 4 cm.
As diagonals of rhombus bisect each other.
∴ BD = 2 OB = 2 × 4 = 8 cm.
cos 30° =
⇒
⇒ OA =
⇒ OA = .
As diagonals of rhombus bisect each other.
∴ AC = 2 OA = .
Hence, the length of the diagonals of the rhombus are 8 cm and cm.
Answered By
30 Likes
Related Questions
If sin x + cos y = 1, x = 30° and y is acute angle, find the value of y.
If sin(A + B) = = cos(A - B), 0° < A + B ≤ 90° (A > B), find the values of A and B.
In the right-angled triangle ABC, ∠C = 90° and ∠B = 60°. If AC = 6 cm, find the lengths of the sides BC and AB.
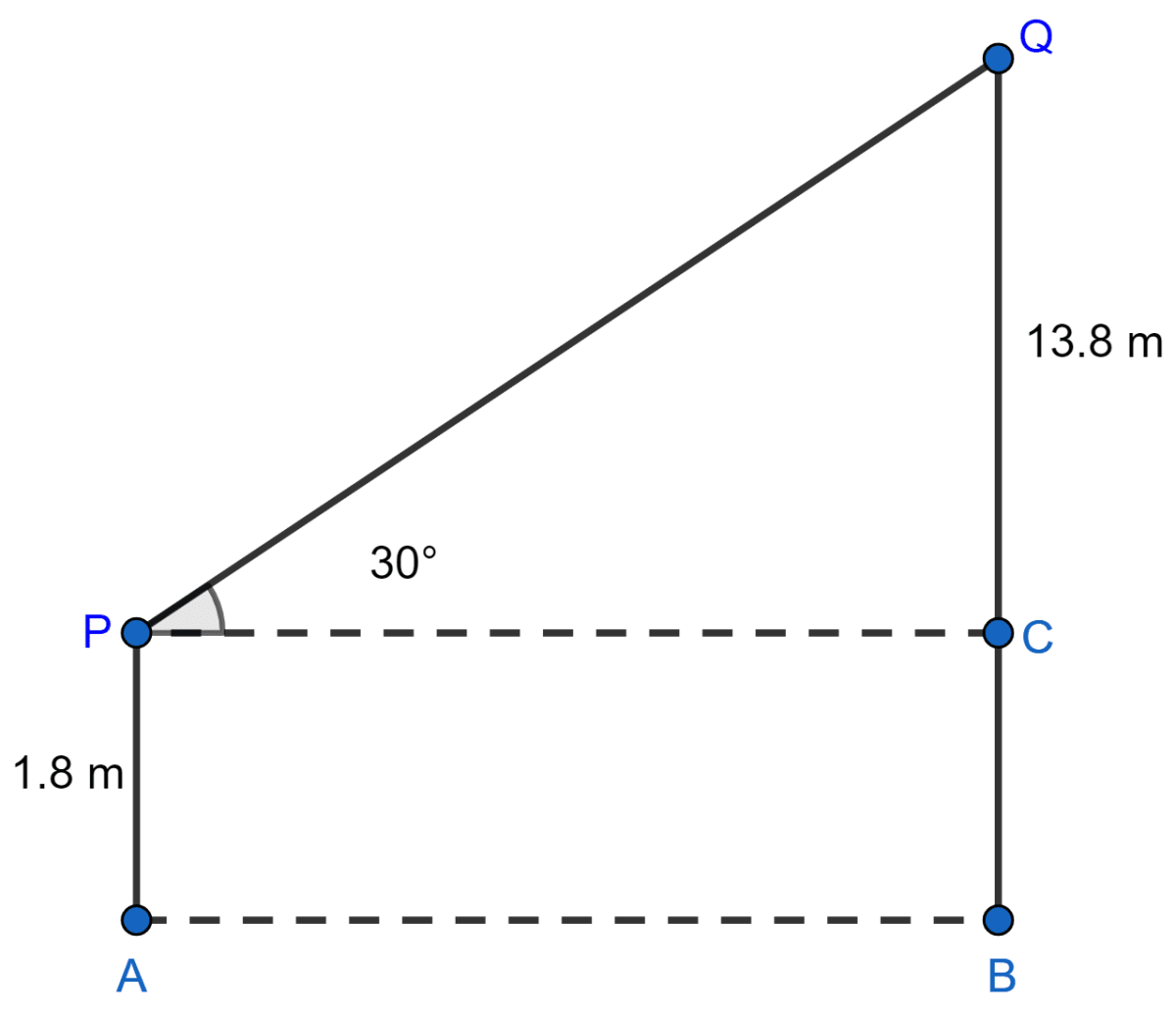
In the adjoining figure, AP is a man of height 1.8 m and BQ is a building 13.8 m high. If the man sees the top of the building by focussing his binoculars at an angle of 30° to the horizontal, find the distance of the man from the building.