Mathematics
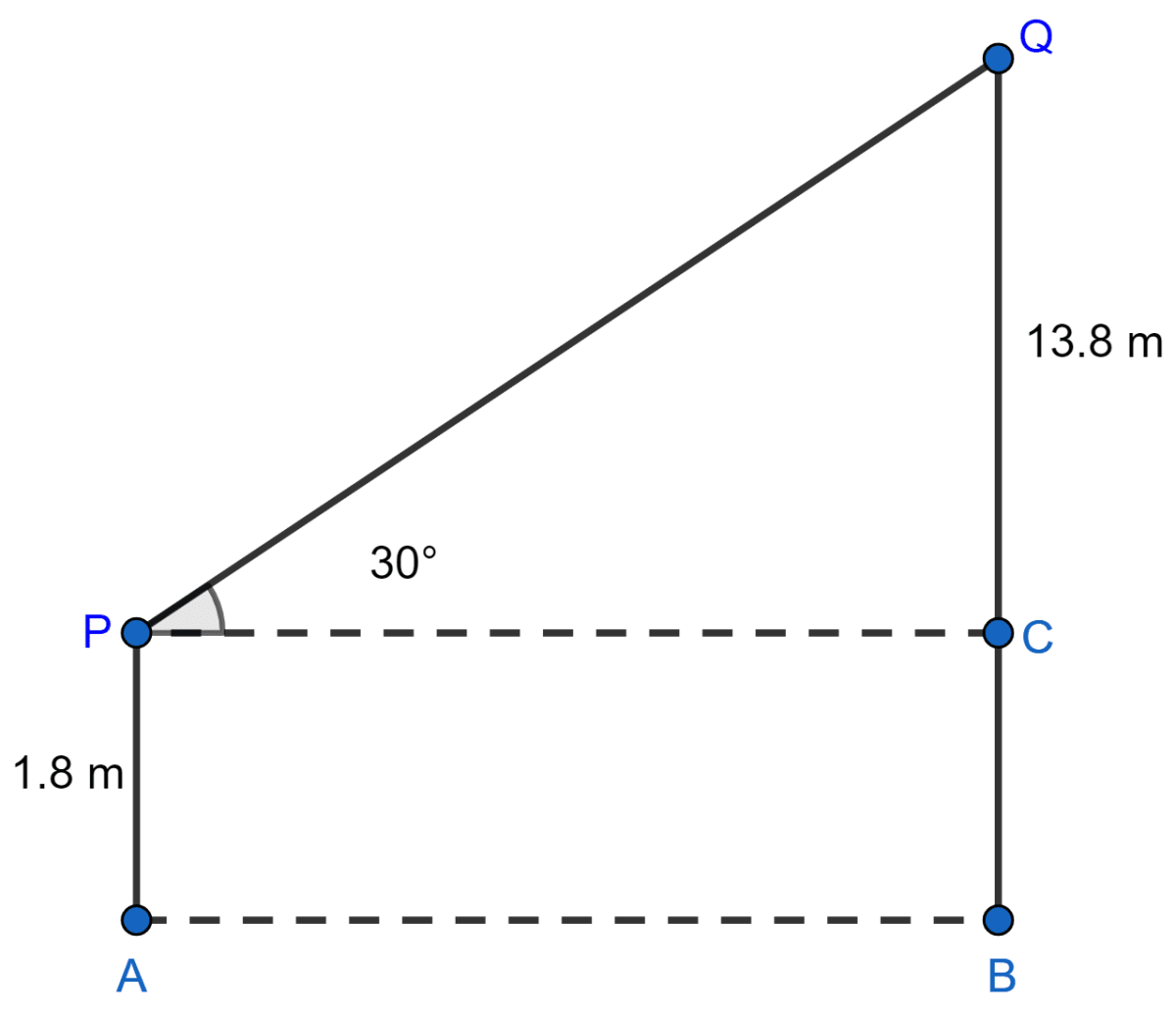
In the adjoining figure, AP is a man of height 1.8 m and BQ is a building 13.8 m high. If the man sees the top of the building by focussing his binoculars at an angle of 30° to the horizontal, find the distance of the man from the building.
Trigonometrical Ratios
56 Likes
Answer
Let AB = d meters, then PC = d meters.
From right-angled △PCQ,
tan 30° =
⇒
From figure,
BC = AP = 1.8 m
⇒
⇒
⇒ d = meters.
Hence, distance of man from building is meters.
Answered By
35 Likes
Related Questions
If the length of each side of a rhombus is 8 cm and its one angle is 60°, then find the lengths of the diagonals of the rhombus.
In the right-angled triangle ABC, ∠C = 90° and ∠B = 60°. If AC = 6 cm, find the lengths of the sides BC and AB.
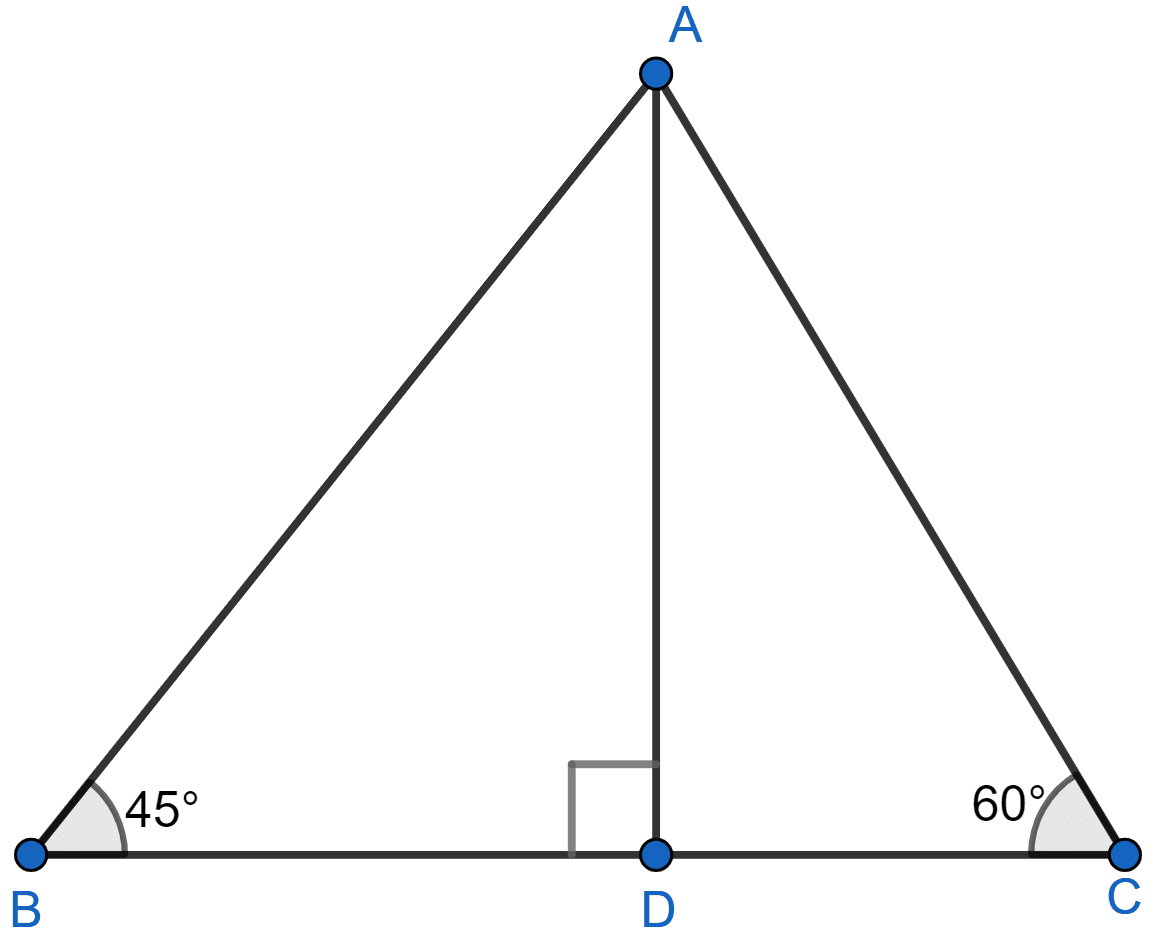
In the adjoining figure, ABC is a triangle in which ∠B = 45° and ∠C = 60°. If AD ⊥ BC and BC = 8m, find the length of the altitude AD.
Without using trigonometric tables, evaluate the following: