Mathematics
If the length and the breadth of a room are increased by 1 metre, the area is increased by 21 square metres. If the length is increased by 1 metre and breadth is decreased by 1 metre the area is decreased by 5 square metres. Find the perimeter of the room.
Answer
Let length = l metres and breadth = b metres.
Area = lb m2
Given,
If the length and the breadth of a room are increased by 1 metre, the area is increased by 21 square metres,
∴ (l + 1)(b + 1) - lb = 21
⇒ lb + l + b + 1 - lb = 21
⇒ l + b = 21 - 1
⇒ l + b = 20 ……….(1)
Given,
If the length is increased by 1 metre and breadth is decreased by 1 metre the area is decreased by 5 square metres.
∴ lb - (l + 1)(b - 1) = 5
⇒ lb - (lb - l + b - 1) = 5
⇒ lb - lb + l - b + 1 = 5
⇒ l - b = 4 ……….(2)
Adding equation (1) and (2) we get,
⇒ l + b + l - b = 20 + 4
⇒ 2l = 24
⇒ l = 12 m.
Substituting value of l in (2) we get,
⇒ 12 - b = 4
⇒ b = 12 - 4 = 8 m.
Perimeter of room = 2(l + b) = 2 × 20 = 40 m.
Hence, perimeter of room = 40 m.
Related Questions
The figure (ii) given below shows a field with the measurements given in metres. Find the area of the field.

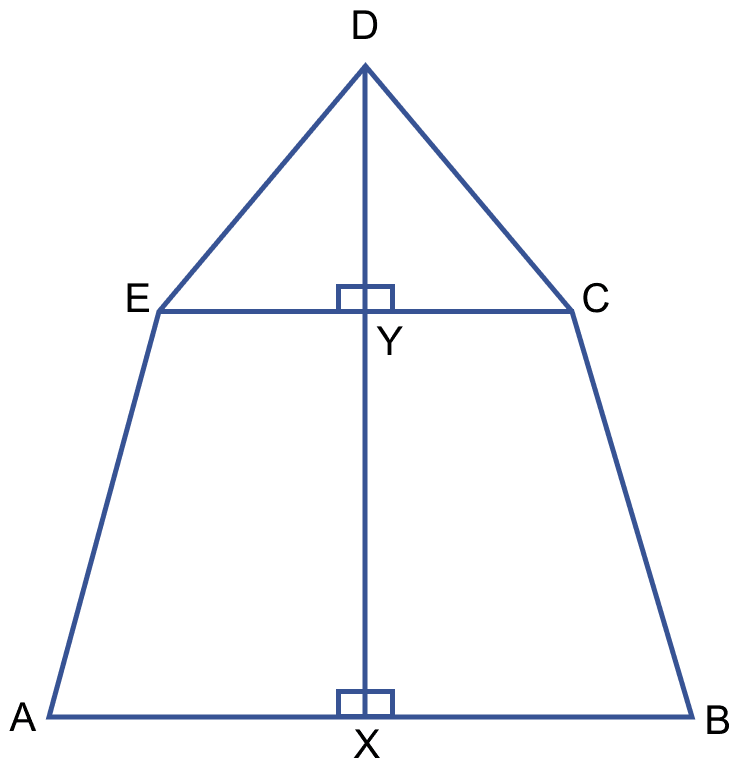
Calculate the area of the pentagon ABCDE shown in fig (iii) below, given that AX = BX = 6 cm, EY = CY = 4 cm, DE = DC = 5 cm, DX = 9 cm and DX is perpendicular to EC and AB.
A triangle and a parallelogram have the same base and same area. If the sides of the triangle are 26 cm, 28 cm and 30 cm, and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
A rectangle of area 105 cm2 has its length equal to x cm. Write down its breadth in terms of x. Given that its perimeter is 44 cm, write down an equation in x and solve it to determine the dimensions of the rectangle.