Mathematics
If a diameter of a circle is perpendicular to one of two parallel chords of the circle, prove that it is perpendicular to the other and bisects it.
Answer
Since, AB || CD and ∠OMA = ∠OMB = 90°
From figure,

∠OMA = ∠OND = 90° (Alternate angles are equal)
∠OMB = ∠ONC = 90° (Alternate angles are equal)
∴ ON ⊥ CD or MN ⊥ CD
We know that,
The perpendicular to a chord from the center of the circle bisects the chord.
∴ NC = ND.
Hence, proved that diameter is perpendicular to other chord and bisects it.
Related Questions
The length of the common chord of two intersecting circles is 30 cm. If the radii of the two circles are 25 cm and 17 cm, find the distance between their centres.
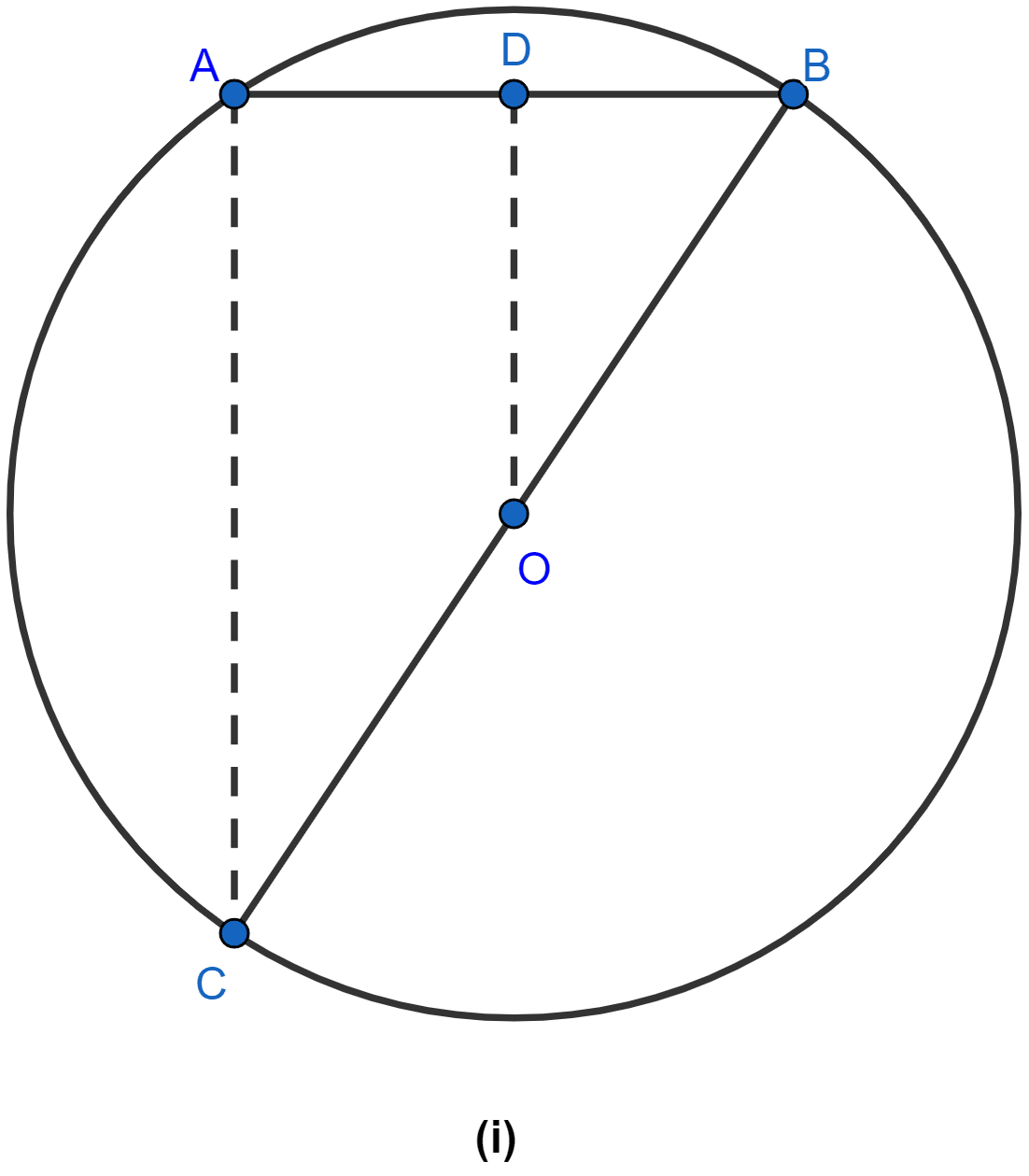
In the figure (i) given below, OD is perpendicular to the chord AB of a circle whose center is O. If BC is a diameter, show that CA = 2OD.
In an equilateral triangle, prove that the centroid and the circumcentre of the triangle coincide.
The line joining mid-points of two chords of a circle passes through its center. Prove that the chords are parallel.