The length of the common chord of two intersecting circles is 30 cm. If the radii of the two circles are 25 cm and 17 cm, find the distance between their centres.

Since, the perpendicular to a chord from the centre of the circle bisects the chord,

∴ AC = CB = $\dfrac{30}{2}$ = 15 cm.

From figure,

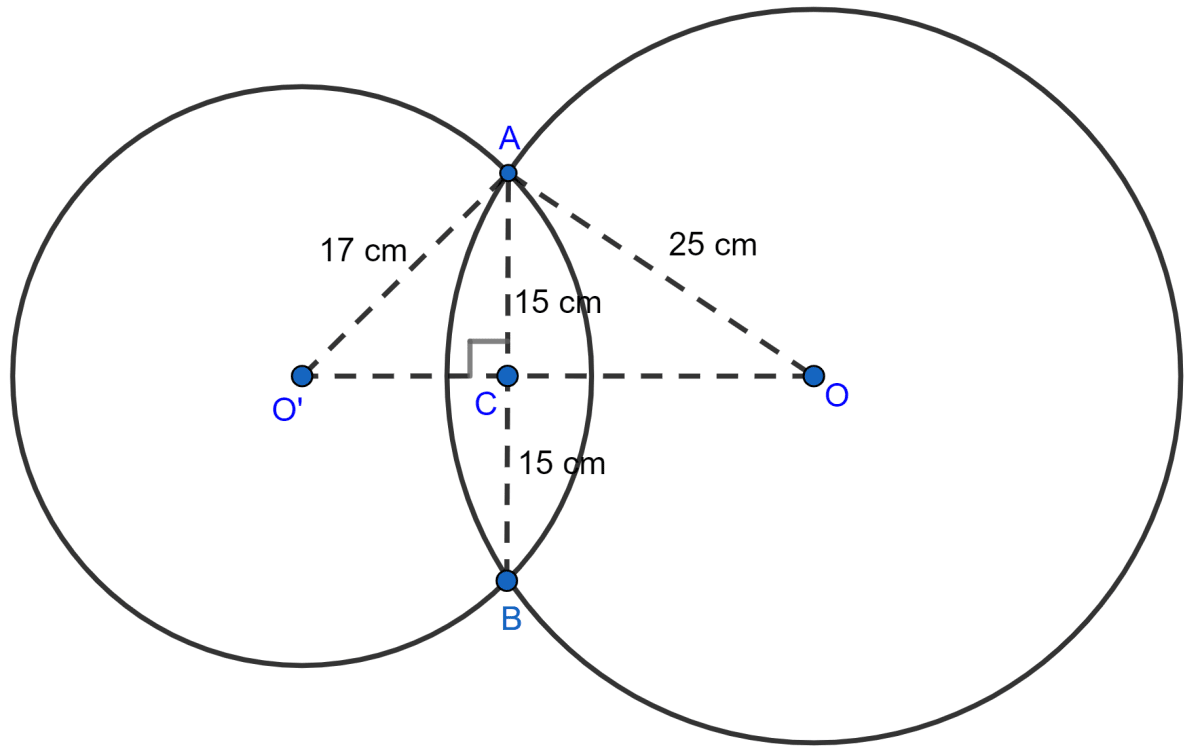
In right triangle OAC,

⇒ OA² = OC² + AC² (By pythagoras theorem)

⇒ 25² = OC² + 15²

⇒ 625 = OC² + 225

⇒ OC² = 400

⇒ OC = $\sqrt{400}$ = 20 cm.

In right triangle O'AC,

⇒ O'A² = O'C² + AC² (By pythagoras theorem)

⇒ 17² = O'C² + 15²

⇒ 289 = O'C² + 225

⇒ O'C² = 64

⇒ O'C = $\sqrt{64}$ = 8 cm.

Distance between centers = OO' = OC + O'C = 20 + 8 = 28 cm.

Hence, distance between their centres = 28 cm.