How does the time period (T) of a simple pendulum depend on its length (l) ? Draw a graph showing the variation of T² with l. How will you use this graph to determine the value of g (acceleration due to gravity)?

Time period of a simple pendulum is directly proportional to the square root of its effective length.

i.e., T ∝ $\sqrt{l}$

Graph showing the variation of T² with l is given below:

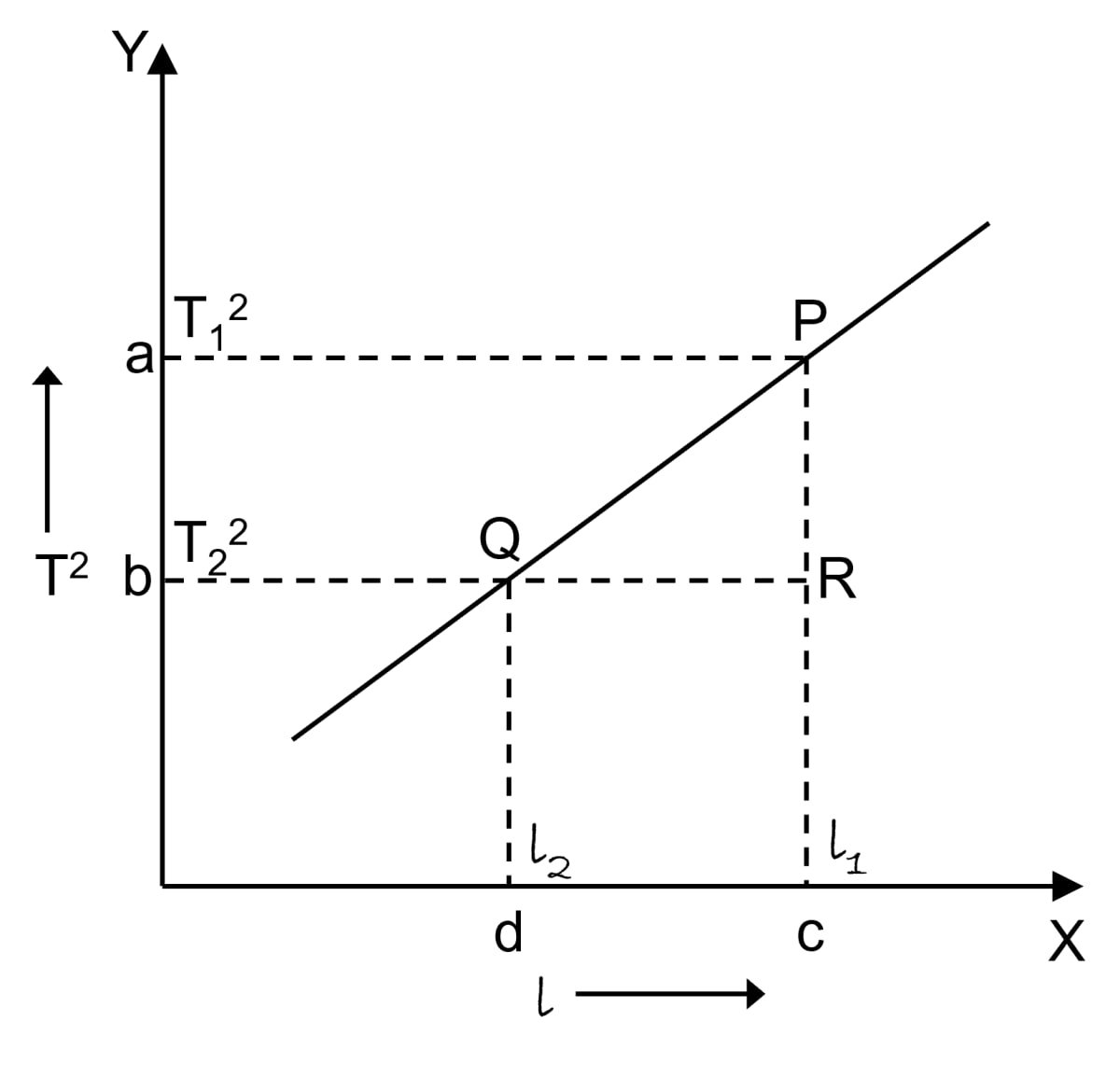
In order to find the acceleration due to gravity with the help of the above graph, we follow the following steps —

The slope of the straight line obtained in the T² vs l graph, as shown in fig, can be obtained by taking two points P and Q on the straight line and drawing normals from these points on the X and Y axes. Then, note the value of T², say T₁² and T₂² at a and b respectively, and also the value of l say l₁ and l₂ respectively at c and d.

Then,

$\text{Slope} = \dfrac{PR}{QR} = \dfrac{ab}{cd} = \dfrac{T$1^2 - T2^2}{l1 - l2}

This slope is found to be a constant at a place and,

$\text{Slope} = \dfrac{4π^2}{g}$

where, g = acceleration due to gravity at that place.

Thus, g can be determined at a place from the graph using the following relation,

$g = \dfrac{4π^2}{\text{Slope of } T^2 \text{ vs l graph}}$