KnowledgeBoat Logo

Mathematics

From the top of a building 20 m high, the angle of elevation of the top of a monument is 45° and the angle of depression of its foot is 15°. Find the height of the monument.

Heights & Distances

75 Likes

Answer

Let AB be the building and CD be the monument. Let length of monument (CD) be h metres.

Let distance between building and monument (BD) be x meters.

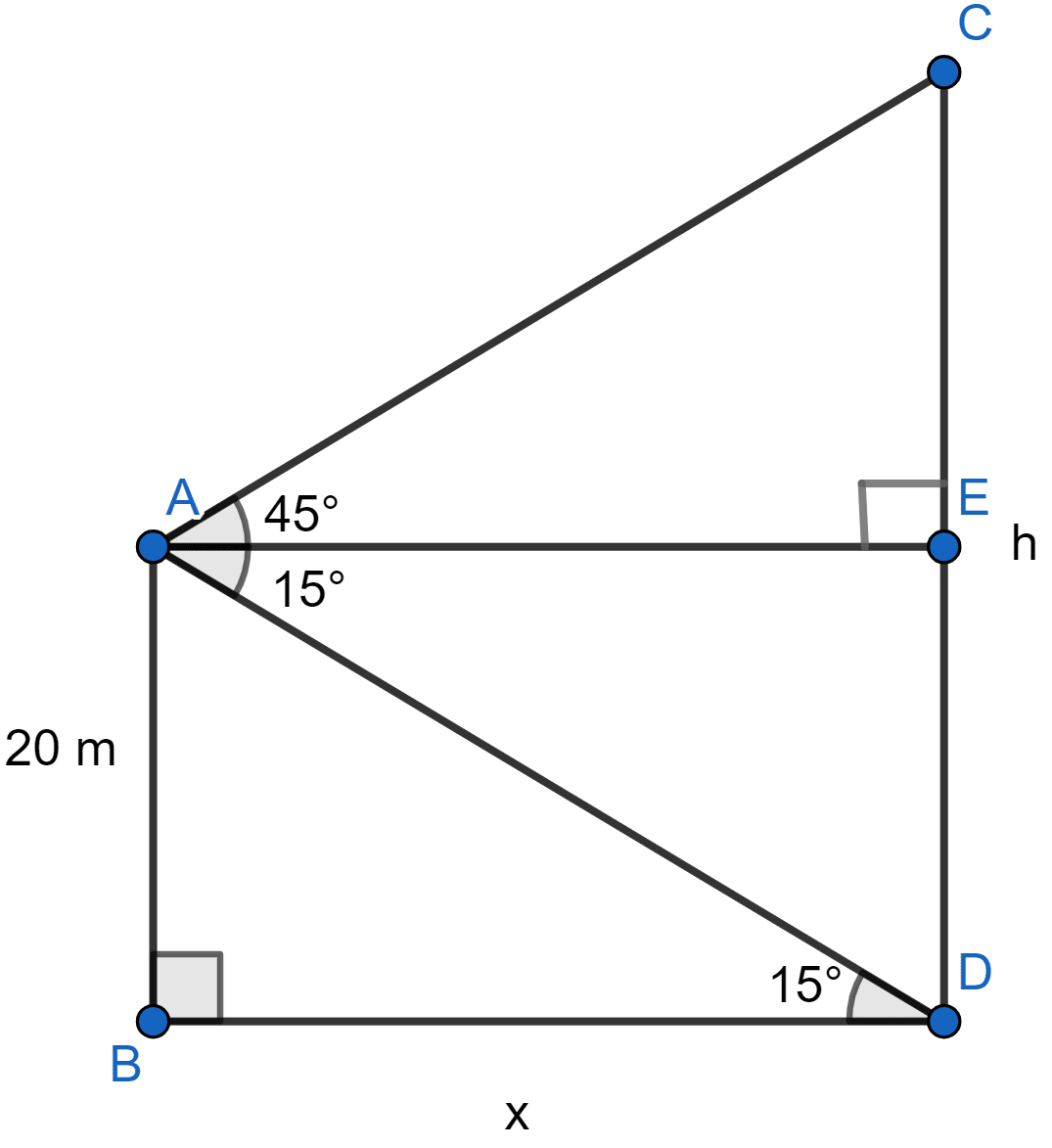
From the top of a building 20 m high, the angle of elevation of the top of a monument is 45° and the angle of depression of its foot is 15°. Find the height of the monument. Heights and Distances, ML Aggarwal Understanding Mathematics Solutions ICSE Class 10.

From figure,

ABDE is a rectangle so,

DE = AB = 20 meters
AE = BD = x meters
CE = CD - DE = (h - 20) meters
∠EAD = ∠ADB = 15°

Considering right angled △ABD we get,

⇒tan 15°=ABBD⇒0.2679=20x⇒x=200.2679⇒x=74.65\Rightarrow \text{tan 15°} = \dfrac{AB}{BD} \\[1em] \Rightarrow 0.2679 = \dfrac{20}{x} \\[1em] \Rightarrow x = \dfrac{20}{0.2679} \\[1em] \Rightarrow x = 74.65

Considering right angled △ACE we get,

⇒tan 45°=CEAE⇒1=h−20x⇒x=h−20⇒74.65=h−20⇒h=74.65+20⇒h=94.65\Rightarrow \text{tan 45°} = \dfrac{CE}{AE} \\[1em] \Rightarrow 1 = \dfrac{h - 20}{x} \\[1em] \Rightarrow x = h - 20 \\[1em] \Rightarrow 74.65 = h - 20 \\[1em] \Rightarrow h = 74.65 + 20 \\[1em] \Rightarrow h = 94.65

Hence, the height of the monument is 94.65 meters.

Answered By

24 Likes

Related Questions