A pole of height 5 m is fixed on the top of a tower. The angle of elevation of the top of pole as observed from a point A on the ground is 60° and the angle of depression of the point A from the top of the tower is 45°. Find the height of the tower. (Take $\sqrt{3} = 1.732$)

Let the height of tower (BC) be h meters and BD be the pole of height 5 meters above it.

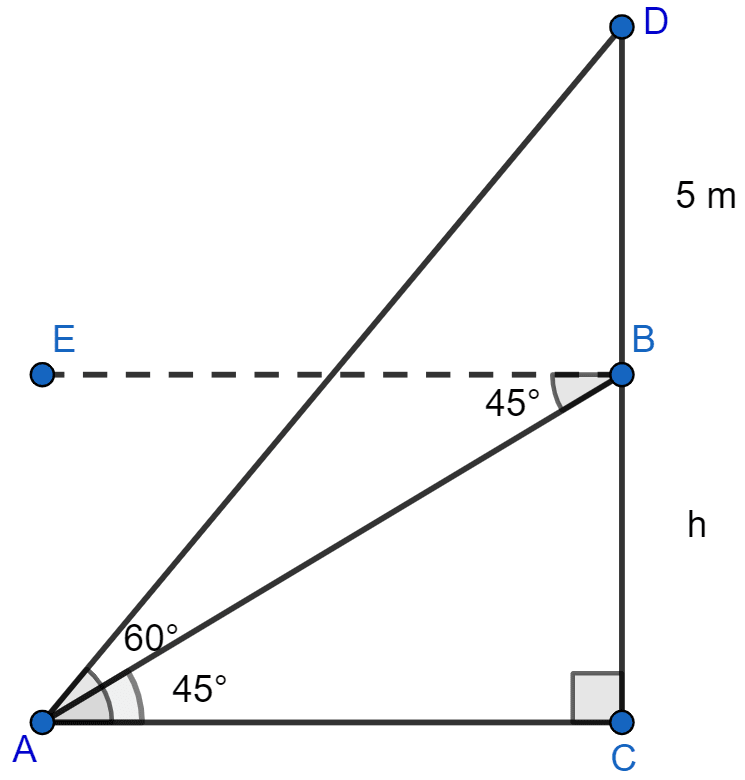
From figure,

∠BAC = ∠EBA = 45° (Alternate angles are equal)

DC = DB + BC = 5 + h.

Considering right angled △BCA, we get

$\Rightarrow \text{tan 45°} = \dfrac{BC}{AC} \\[1em] \Rightarrow 1 = \dfrac{h}{AC} \\[1em] \Rightarrow AC = h \text{ ……(Eq 1)}$

Considering right angled △DCA, we get

$\Rightarrow \text{tan 60°} = \dfrac{DC}{AC} \\[1em] \Rightarrow \sqrt{3} = \dfrac{h + 5}{AC}$

Putting value of AC from Eq 1 in above equation we get,

$\Rightarrow \sqrt{3} = \dfrac{h + 5}{h} \\[1em] \Rightarrow \sqrt{3}h = h + 5 \\[1em] \Rightarrow \sqrt{3}h - h = 5 \\[1em] \Rightarrow 0.732\text{ h} = 5 \\[1em] \Rightarrow h = \dfrac{5}{0.732} \\[1em] \Rightarrow h = 6.83$

Hence, the height of the tower is 6.83 meters.