Mathematics
From the top of a building 20 m high, the angle of elevation of the top of a monument is 45° and the angle of depression of its foot is 15°. Find the height of the monument.
Heights & Distances
Answer
Let AB be the building and CD be the monument. Let length of monument (CD) be h metres.
Let distance between building and monument (BD) be x meters.
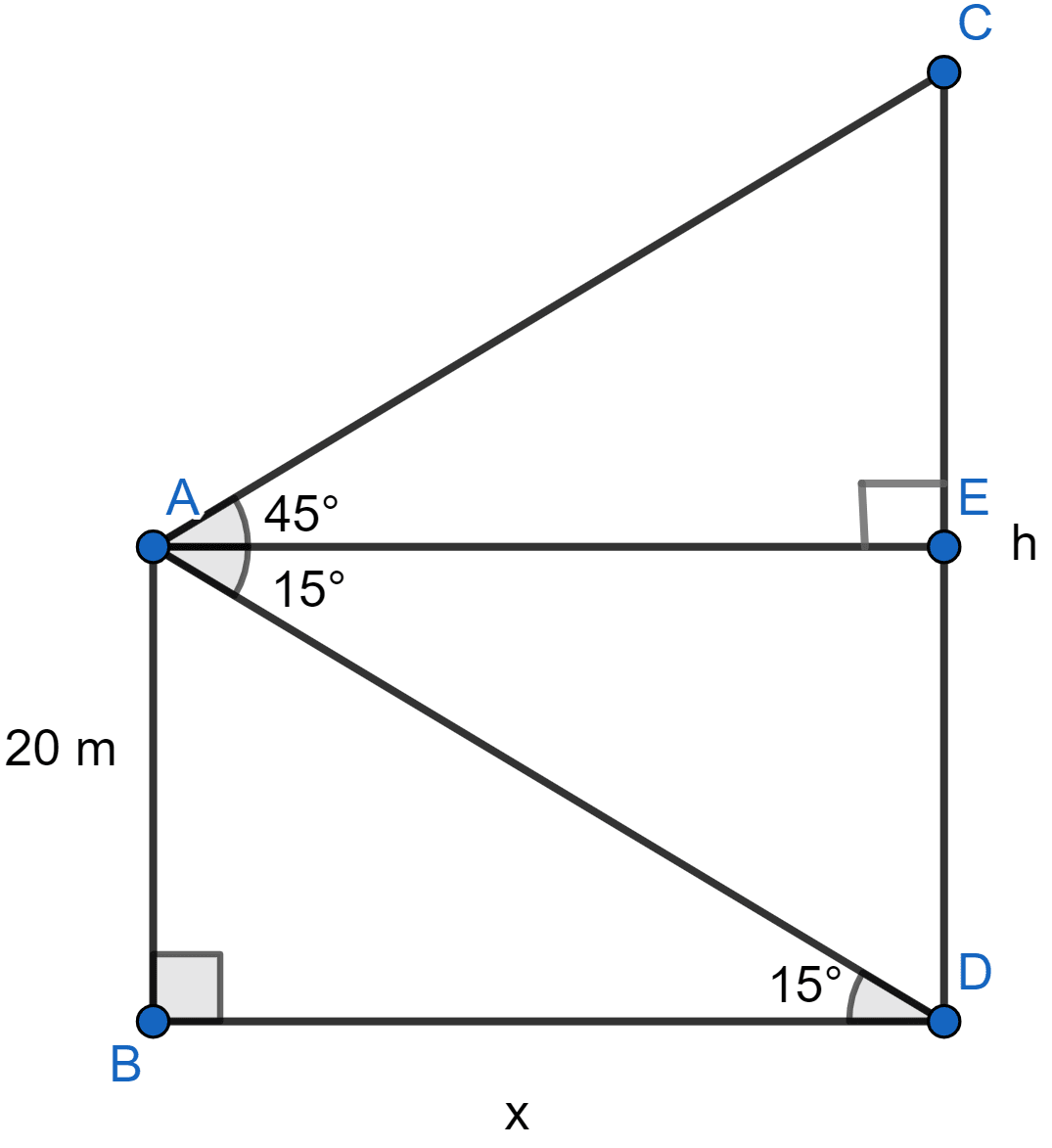
From figure,
ABDE is a rectangle so,
DE = AB = 20 meters
AE = BD = x meters
CE = CD - DE = (h - 20) meters
∠EAD = ∠ADB = 15°
Considering right angled △ABD we get,
Considering right angled △ACE we get,
Hence, the height of the monument is 94.65 meters.
Answered By
Related Questions
A pole of height 5 m is fixed on the top of a tower. The angle of elevation of the top of pole as observed from a point A on the ground is 60° and the angle of depression of the point A from the top of the tower is 45°. Find the height of the tower. (Take )
A vertical pole and a vertical tower are on the same level ground. From the top of the pole, the angle of elevation of the top of the tower is 60° and the angle of depression of the foot of tower is 30°. Find the height of the tower if the height of the pole is 20 m.
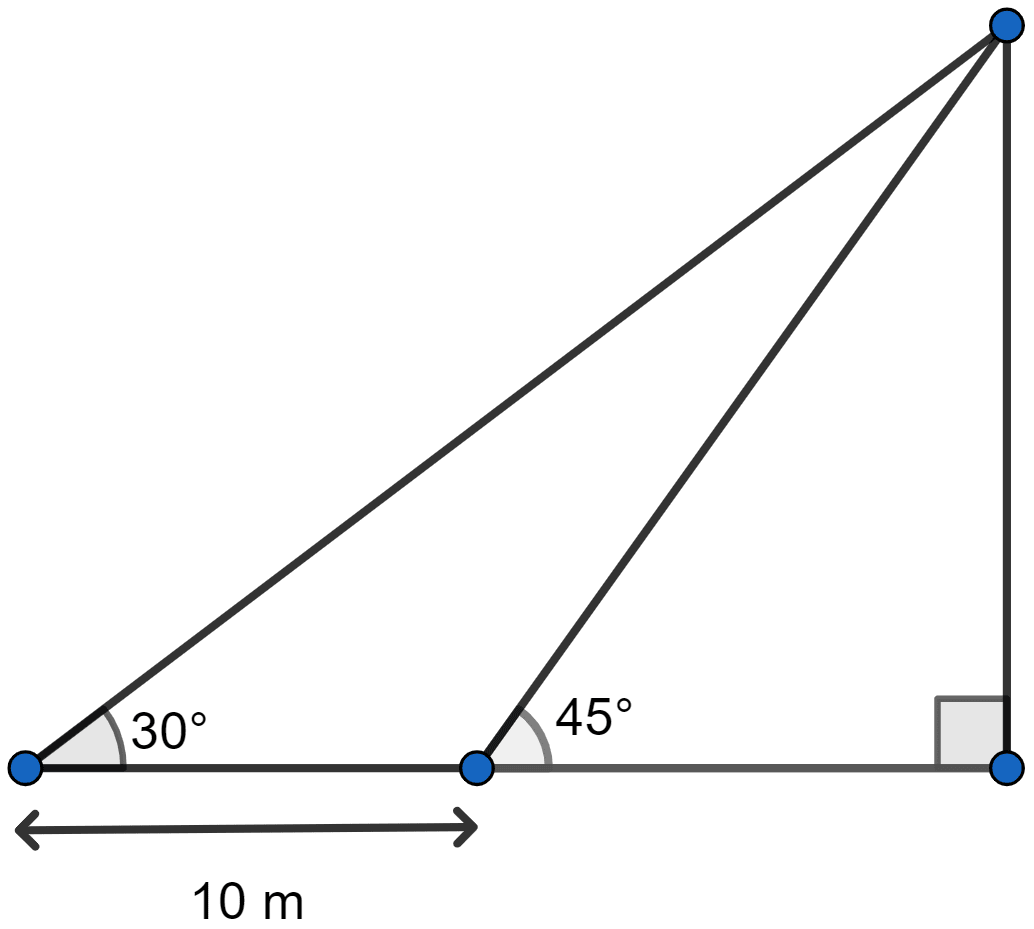
In the adjoining figure, the shadow of a vertical tower on the level ground increases by 10 m, when the altitude of the sun changes from 45° to 30°. Find the height of the tower and give your answer, correct to of a metre.
An aircraft is flying at a constant height with a speed of 360 km/h. From a point on the ground, the angle of elevation of the aircraft at an instant was observed to be 45°. After 20 seconds, the angle of elevation was observed to be 30°. Determine the height at which the aircraft is flying (use = 1.732).