Mathematics
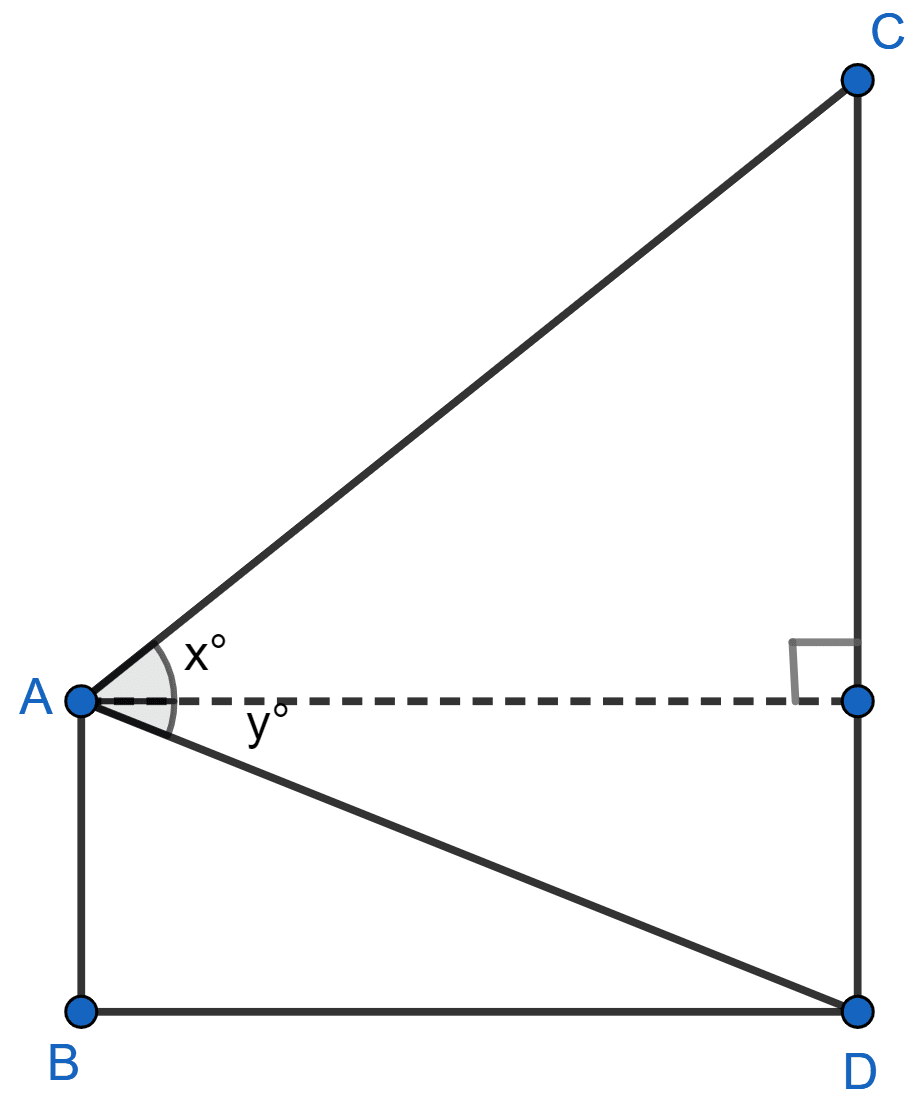
From a window A, 10 m above the ground the angle of elevation of the top C of a tower is x°, where tan x° = and the angle of depression of the foot D of the tower is y°, where tan y° = . Calculate the height CD of the tower in metres.
Heights & Distances
Answer
From figure,
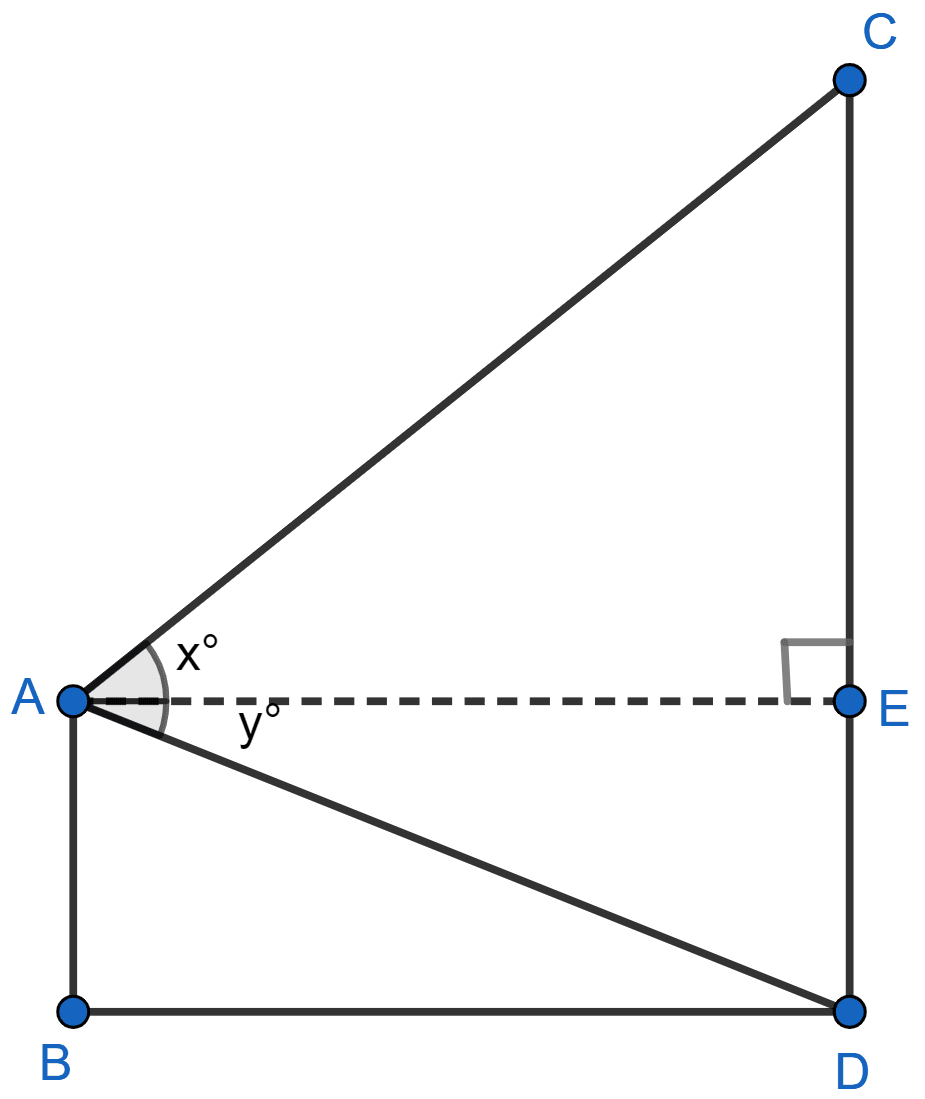
⇒ AB = DE = 10 m.
In ∆AED
In ∆AEC,
From figure,
CD = DE + CE = 10 + 100 = 110 m.
Hence, height of tower (CD) = 110 m.
Answered By
Related Questions
A vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height h meter. At a point on the plane, the angle of elevation of the bottom of the flagstaff is α and at the top of the flagstaff is β. Prove that the height of the tower is .
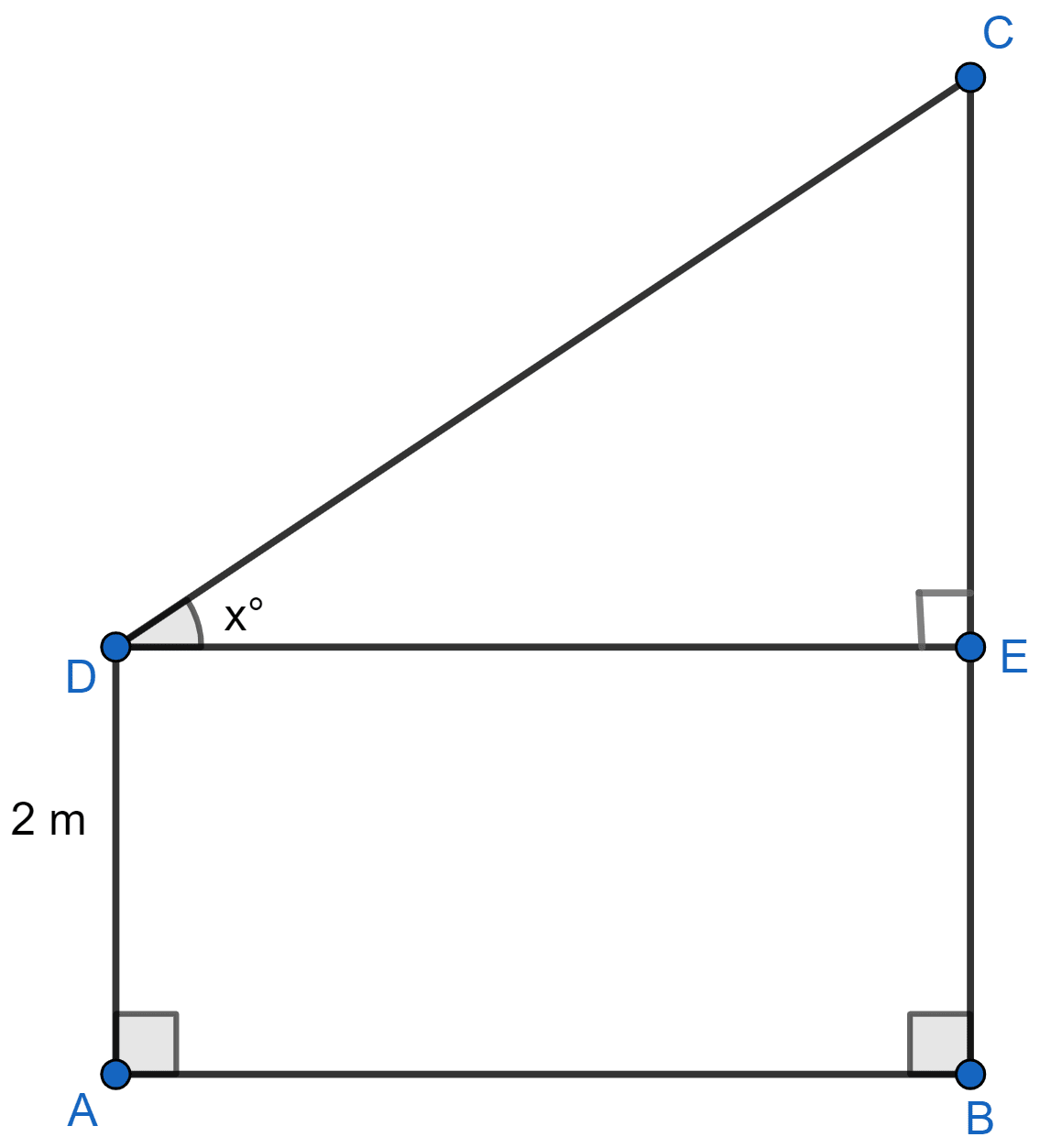
With reference to the given figure, a man stands on the ground at point A, which is on the same horizontal plane as B, the foot of the vertical pole BC. The height of the pole is 10 m. The man's eye is 2 m above the ground. He observes the angle of elevation of C, the top of the pole, as x°, where tan x° = . Calculate:
(i) the distance AB in metres;
(ii) angle of elevation of the top of the pole when he is standing 15 metres from the pole. Give your answer to the nearest degree.
A vertical tower is 20 m high. A man standing at some distance from the tower knows that the cosine of the angle of elevation of the top of the tower is 0.53. How far is he standing from the foot of the tower ?
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole the angle of elevation of the top of the tower is 60° and the angle of depression of the bottom of the tower is 30°. Find :
(i) the height of the tower, if the height of the pole is 20 m;
(ii) the height of the pole, if the height of the tower is 75 m