Mathematics
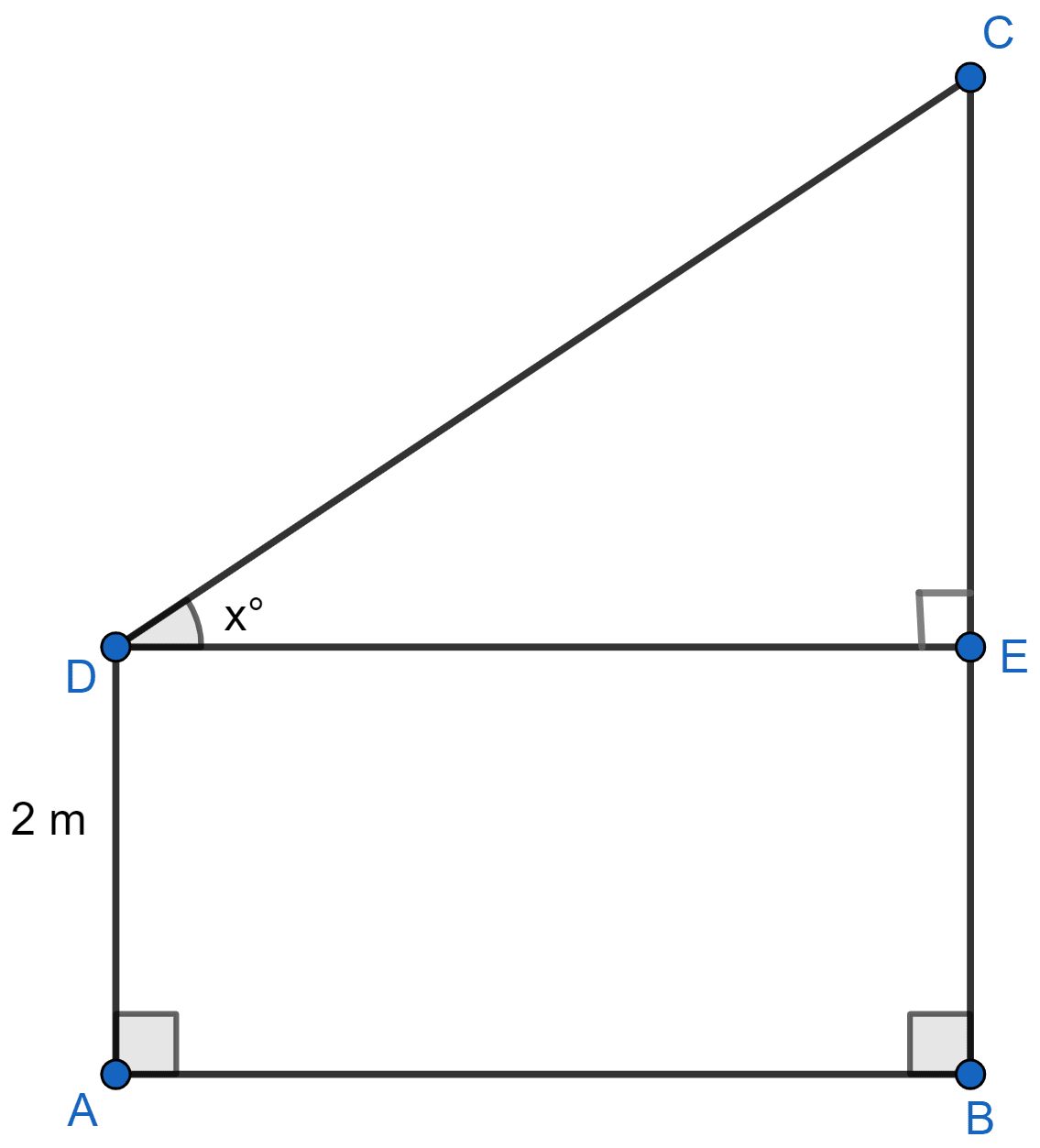
With reference to the given figure, a man stands on the ground at point A, which is on the same horizontal plane as B, the foot of the vertical pole BC. The height of the pole is 10 m. The man's eye is 2 m above the ground. He observes the angle of elevation of C, the top of the pole, as x°, where tan x° = . Calculate:
(i) the distance AB in metres;
(ii) angle of elevation of the top of the pole when he is standing 15 metres from the pole. Give your answer to the nearest degree.
Heights & Distances
8 Likes
Answer
Let's take AD to be the height of the man, AD = 2 m.
From figure, BE = AD = 2 m.
Also,
CE = BC - BE = (10 - 2) = 8 m.
(i) In ∆CED,
From figure,
AB = DE = 20 m.
Hence, AB = 20 m.
(ii) Let A'D' be the new position of the man and θ be the angle of elevation of the top of the tower.
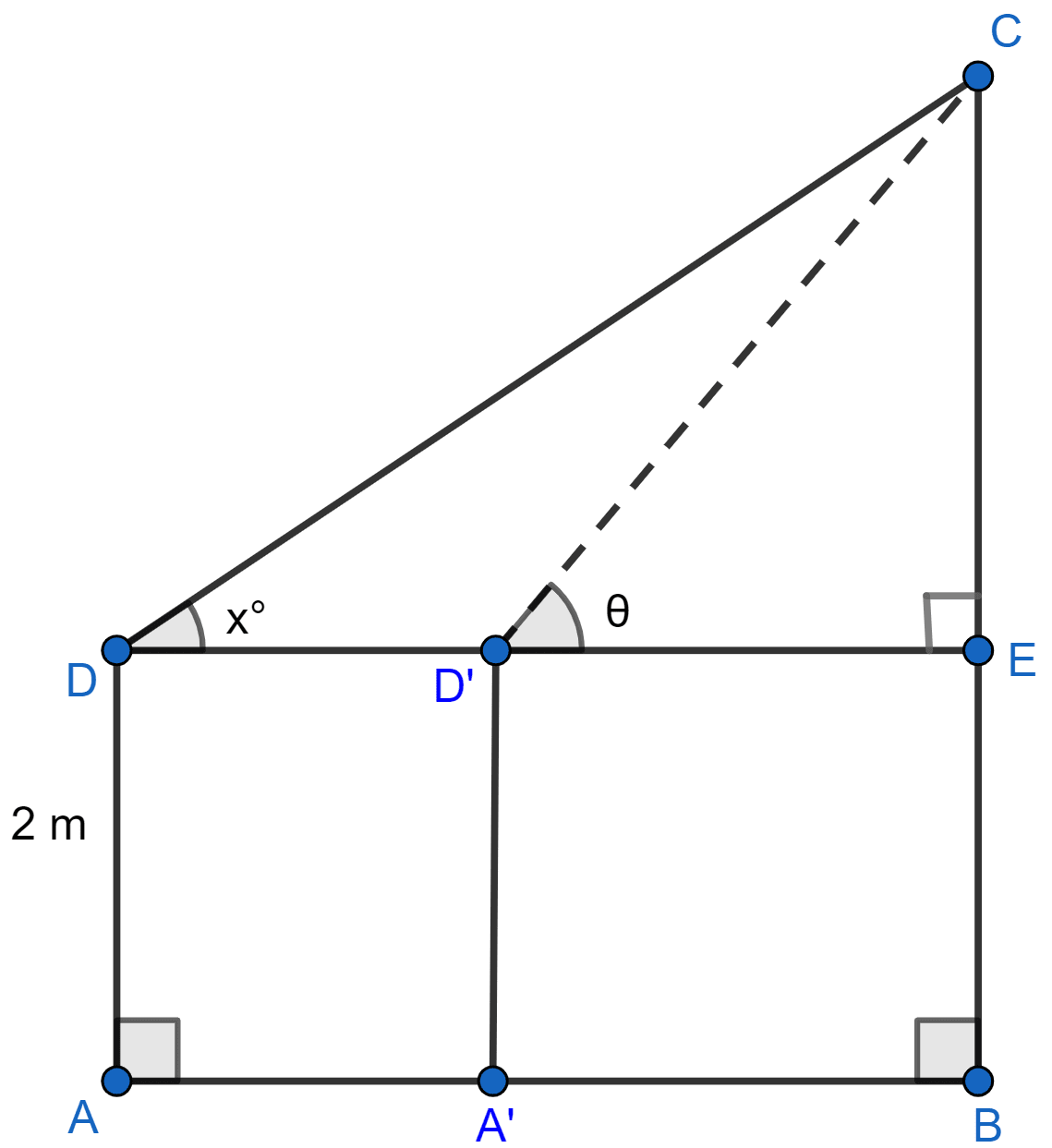
Such that, D'E = 15 m
In ∆CED',
Hence, angle of elevation of the top of the pole when the man is standing 15 metres from the pole is 28°.
Answered By
2 Likes
Related Questions
At a point on level ground, the angle of elevation of a vertical tower is found to be such that its tangent is . On walking 192 meters towards the tower; the tangent of the angle is found to be . Find the height of the tower.
A vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height h meter. At a point on the plane, the angle of elevation of the bottom of the flagstaff is α and at the top of the flagstaff is β. Prove that the height of the tower is .
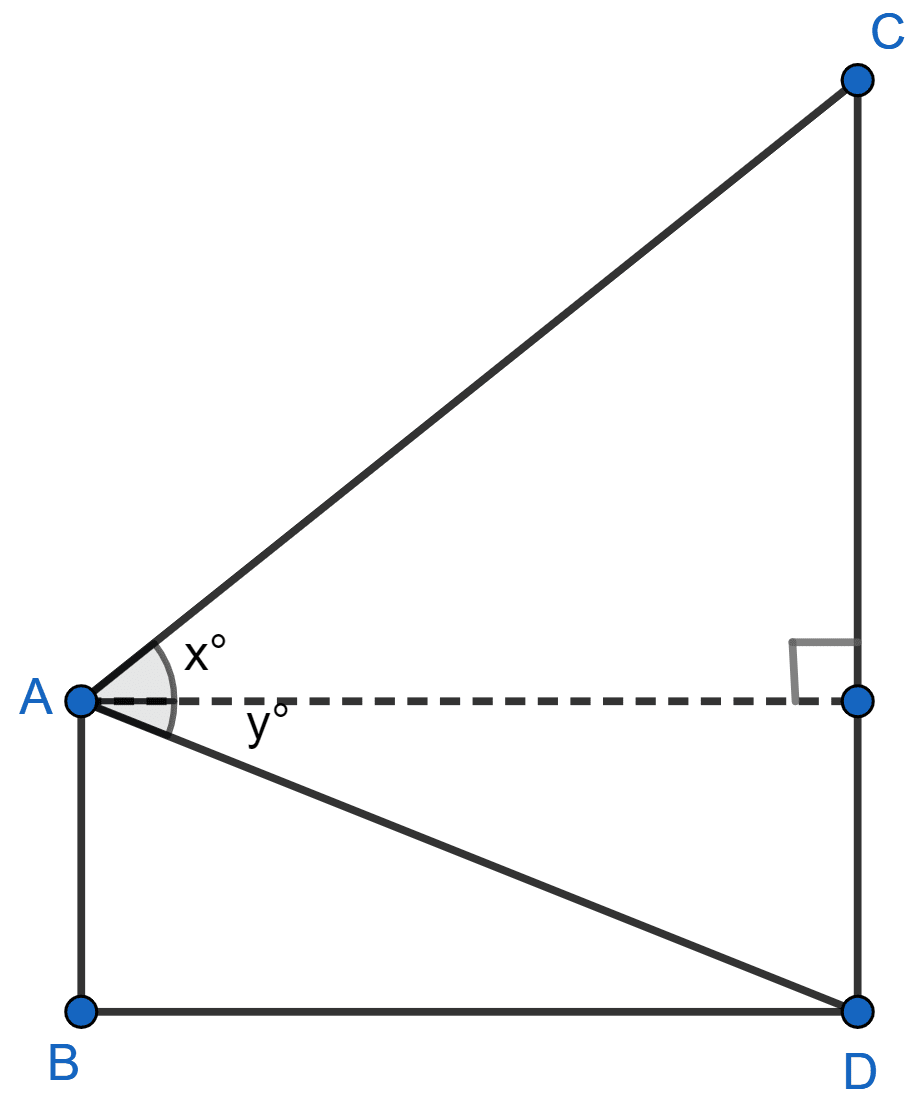
From a window A, 10 m above the ground the angle of elevation of the top C of a tower is x°, where tan x° = and the angle of depression of the foot D of the tower is y°, where tan y° = . Calculate the height CD of the tower in metres.
A vertical tower is 20 m high. A man standing at some distance from the tower knows that the cosine of the angle of elevation of the top of the tower is 0.53. How far is he standing from the foot of the tower ?