Find the area of an isosceles triangle whose equal sides are 12 cm each and the perimeter is 30 cm.

Consider △ABC as the isosceles triangle.

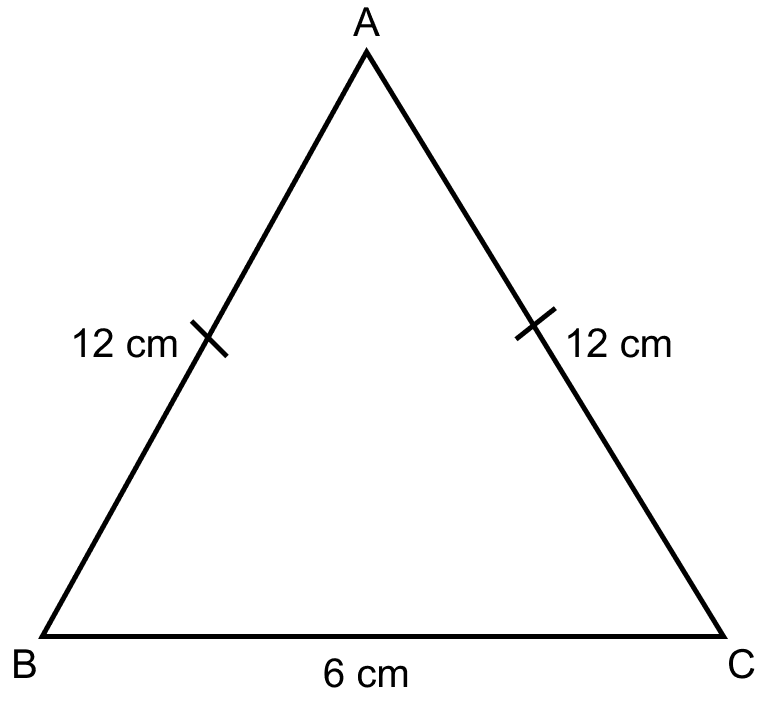
Here, AB = AC = 12 cm.

Perimeter = 30 cm

⇒ AB + AC + BC = 30

⇒ 12 + 12 + BC = 30

⇒ BC = 30 - 24 = 6 cm.

We know that,

Semi-perimeter (s) = $\dfrac{\text{Perimeter}}{2} = \dfrac{30}{2}$ = 15 cm.

Area of an isosceles triangle = $\dfrac{1}{4}b\sqrt{4a^2 - b^2}$, where a is length of equal sides and b is the length of other side.

Substituting values we get,

$A = \dfrac{1}{4} \times 6 \times \sqrt{4(12)^2 - 6^2} \\[1em] = \dfrac{1}{4} \times 6 \times \sqrt{4 \times 144 - 36} \\[1em] = \dfrac{1}{4} \times 6 \times \sqrt{540} \\[1em] = \dfrac{1}{4} \times 6 \times 23.24 \\[1em] = \dfrac{139.44}{6} \\[1em] = 34.86 \text{ cm}^2.$

Hence, area of isosceles triangle = 34.86 cm².