ABC is a triangle in which AB = AC = 4 cm and ∠A = 90°. Calculate the area of △ABC. Also find the length of perpendicular from A to BC.

It is given that

AB = AC = 4 cm

From figure,

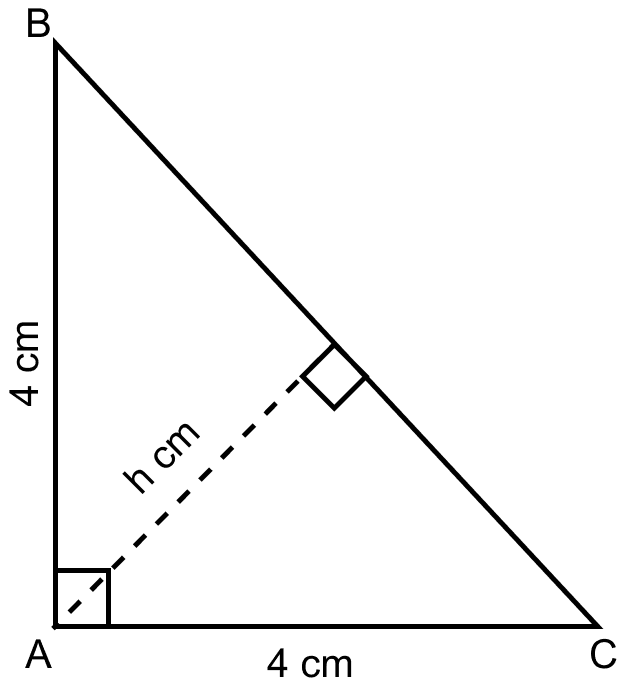
Using the Pythagoras theorem,

BC² = AB² + AC²

Substituting the values we get,

⇒ BC² = 4² + 4²

⇒ BC² = 16 + 16 = 32

⇒ BC = $\sqrt{32} = 4\sqrt{2}$ cm.

Let perpendicular from A to BC be h cm.

Area of △ABC = $\dfrac{1}{2}$ × base × height

= $\dfrac{1}{2}$ × AC × AB

= $\dfrac{1}{2} \times 4 \times 4$

= 8 cm.

From figure,

Area of △ABC = $\dfrac{1}{2}$ × BC × h.

$\therefore 8 = \dfrac{1}{2} \times BC \times h \\[1em] \Rightarrow 8 = \dfrac{1}{2} \times 4\sqrt{2} \times h \\[1em] \Rightarrow 8 = 2\sqrt{2}h \\[1em] \Rightarrow h = \dfrac{8}{2\sqrt{2}} \\[1em] \Rightarrow h = 2\sqrt{2} = 2.83$

Hence, area of △ABC = 8 cm² and length of perpendicular from A to BC = 2.83 cm.