Mathematics
Find the area of an isosceles triangle whose equal sides are 12 cm each and the perimeter is 30 cm.
Mensuration
46 Likes
Answer
Consider △ABC as the isosceles triangle.
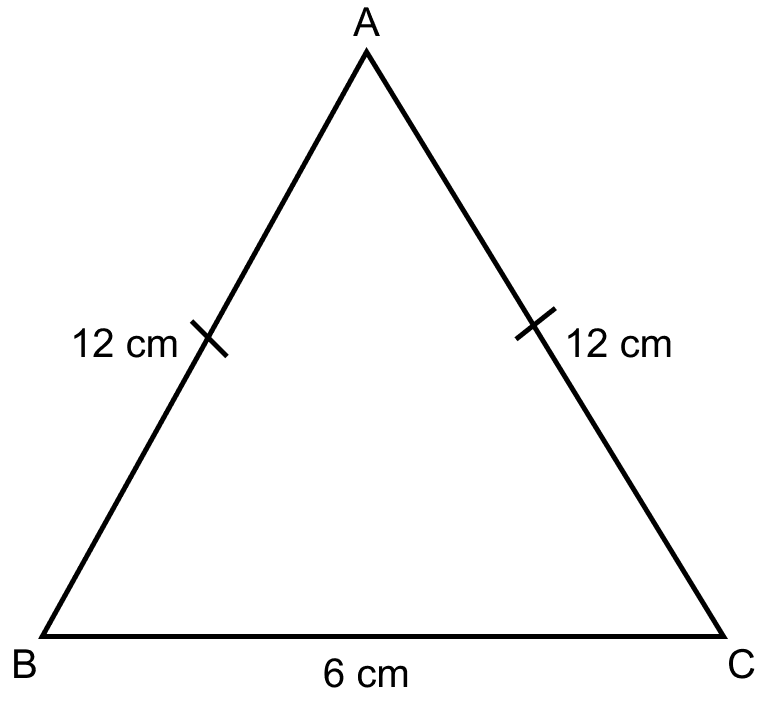
Here, AB = AC = 12 cm.
Perimeter = 30 cm
⇒ AB + AC + BC = 30
⇒ 12 + 12 + BC = 30
⇒ BC = 30 - 24 = 6 cm.
We know that,
Semi-perimeter (s) = = 15 cm.
Area of an isosceles triangle = , where a is length of equal sides and b is the length of other side.
Substituting values we get,
Hence, area of isosceles triangle = 34.86 cm2.
Answered By
15 Likes
Related Questions
The sides of a triangular plot are in the ratio 3 : 5 : 7 and its perimeter is 300 m. Find its area. Take .
ABC is a triangle in which AB = AC = 4 cm and ∠A = 90°. Calculate the area of △ABC. Also find the length of perpendicular from A to BC.
Find the area of an isosceles triangle whose base is 6 cm and perimeter is 16 cm.
The sides of a right-angled triangle containing the right angle are 5x cm and (3x – 1) cm. Calculate the length of the hypotenuse of the triangle if its area is 60 cm2.