Mathematics
Find the area enclosed by the figure (i) given below, where ABC is an equilateral triangle and DEFG is an isosceles trapezium. All measurements are in centimeters.
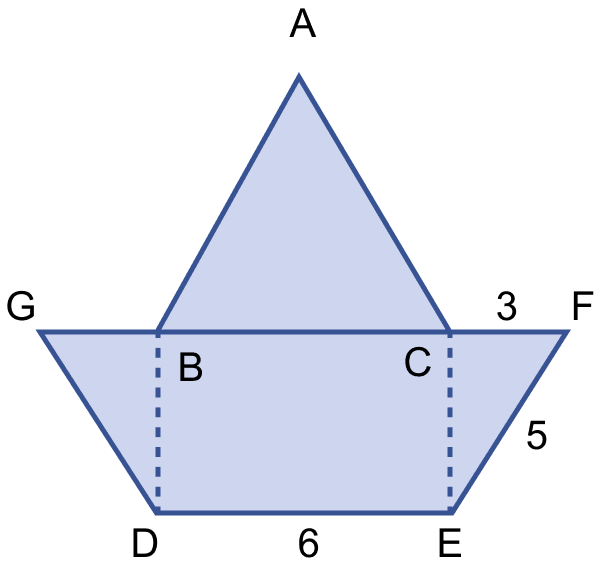
Mensuration
25 Likes
Answer
In right angle triangle ECF,
Using pythagoras theorem,
⇒ EF2 = EC2 + CF2
⇒ 52 = EC2 + 32
⇒ EC2 = 52 - 32
⇒ EC2 = 25 - 9 = 16
⇒ EC = = 4 cm.
Since, DEFG is an isosceles trapezium.
∴ GD = EF= 5 cm.
Since, BDEC is a rectangle,
∴ BD = EC = 4 cm and BC = DE = 6 cm.
In right angle triangle DBG,
Using pythagoras theorem,
⇒ GD2 = BD2 + GB2
⇒ 52 = 42 + GB2
⇒ GB2 = 52 - 42
⇒ GB2 = 25 - 16 = 9
⇒ GB = = 3 cm.
In trapezium,
GF = GB + BC + CF = 3 + 6 + 3 = 12 cm.
Area of trapezium DEFG = (sum of parallel sides) × distance between them
=
= 18 × 2
= 36 cm2.
Area of equilateral triangle ABC =
=
=
= 1.732 × 9
= 15.59 cm2
Area of figure = Area of trapezium DEFG + Area of equilateral triangle ABC
= 36 + 15.59 = 51.59 cm2.
Hence, area of figure = 51.59 cm2.
Answered By
12 Likes
Related Questions
The perimeter of a square is 48 cm. The area of a rectangle is 4 cm2 less than the area of the square. If the length of the rectangle is 4 cm greater than its breadth, find the perimeter of the rectangle.
In the adjoining figure, ABCD is a rectangle with sides AB = 10 cm and BC = 8 cm. HAD and BFC are equilateral triangles; AEB and DCG are right angled isosceles triangles. Find the area of the shaded region and the perimeter of the figure.
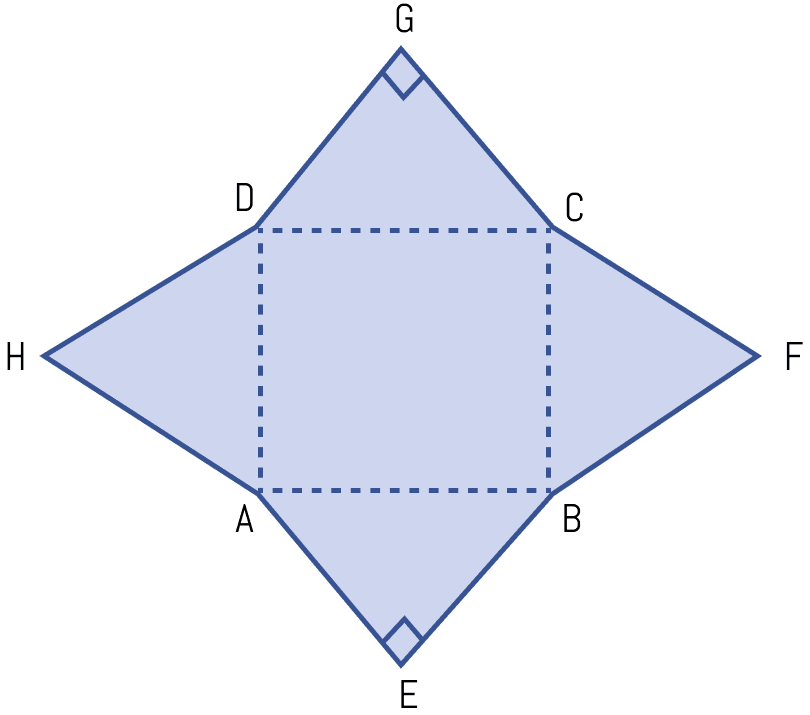
Find the area enclosed by the figure (ii) given below. All measurements are in centimeters.

In the figure (iii) given below, from a 24 cm × 24 cm piece of cardboard, a block in the shape of letter M is cut off. Find the area of the cardboard left over, all measurements are in centimetres.
