Mathematics
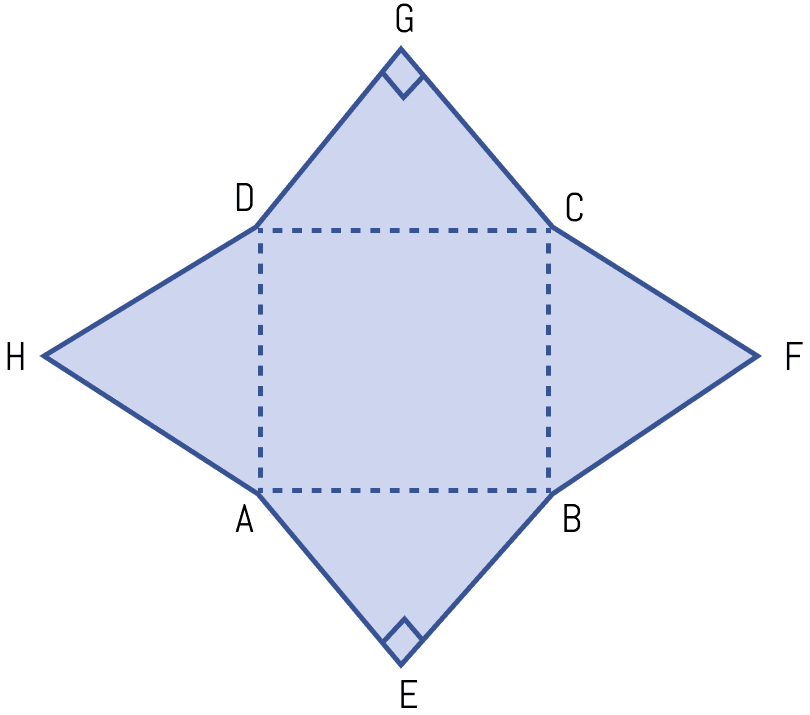
In the adjoining figure, ABCD is a rectangle with sides AB = 10 cm and BC = 8 cm. HAD and BFC are equilateral triangles; AEB and DCG are right angled isosceles triangles. Find the area of the shaded region and the perimeter of the figure.
Mensuration
27 Likes
Answer
In △AEB,
Let AE = BE = x cm, then from right angled triangle AEB,
⇒ AB2 = AE2 + EB2
⇒ 102 = x2 + x2
⇒ 2x2 = 100
⇒ x2 = 50
⇒ x = cm.
Area of right angled △AEB = × base × height
In △DGC,
Let DG = GC = y cm, then from right angled triangle DGC,
⇒ DC2 = DG2 + GC2
⇒ 102 = y2 + y2
⇒ 2y2 = 100
⇒ y2 = 50
⇒ y = cm
Area of right angled △DCG = × base × height
Since, HAD and BFC are equilateral triangle with side = 8 cm.
Area of HAD = Area of BFC = × (side)2
=
= cm2
Area of rectangle ABCD = l × b = AB × CD
= 10 × 8 = 80 cm2
From figure,
Area of shaded region = Area of (△DGC + △BFC + △AEB + △HAD + rectangle ABCD)
= cm2.
Perimeter of figure = (AE + EB + BF + FC + CG + GD + DH + HA)
=
= cm.
Hence, area of shaded region = and perimeter = cm.
Answered By
12 Likes
Related Questions
A rectangle has twice the area of a square. The length of the rectangle is 12 cm greater and the width is 8 cm greater than a side of a square. Find the perimeter of the square.
The perimeter of a square is 48 cm. The area of a rectangle is 4 cm2 less than the area of the square. If the length of the rectangle is 4 cm greater than its breadth, find the perimeter of the rectangle.
Find the area enclosed by the figure (i) given below, where ABC is an equilateral triangle and DEFG is an isosceles trapezium. All measurements are in centimeters.
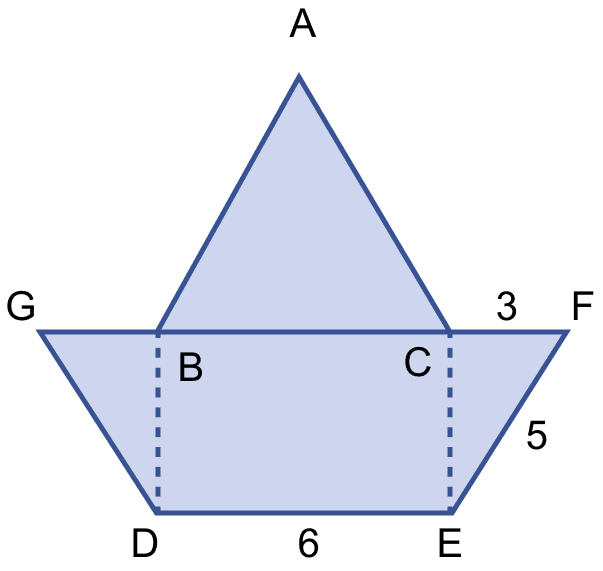
Find the area enclosed by the figure (ii) given below. All measurements are in centimeters.
