Mathematics
Draw the graph of 5x + 6y - 30 = 0 and use it to find the area of the triangle formed by the line and coordinate axes.
Coordinate Geometry
27 Likes
Answer
The above equation, 5x + 6y - 30 = 0 can be written as :
⇒ 6y = -5x + 30
⇒ y =
⇒ y = .
When x = 0, y = - = 0 + 5 = 5,
x = 6, y = - = -5 + 5 = 0,
x = 12, y = - + 5 = -10 + 5 = -5.
Table of values :
| x | y |
|---|---|
| 0 | 5 |
| 6 | 0 |
| 12 | -5 |
Steps of construction :
Plot the points (0, 5), (6, 0) and (12, -5) on the graph.
Connect any two points by a straight line.
Observe that the third point lies on the straight line.
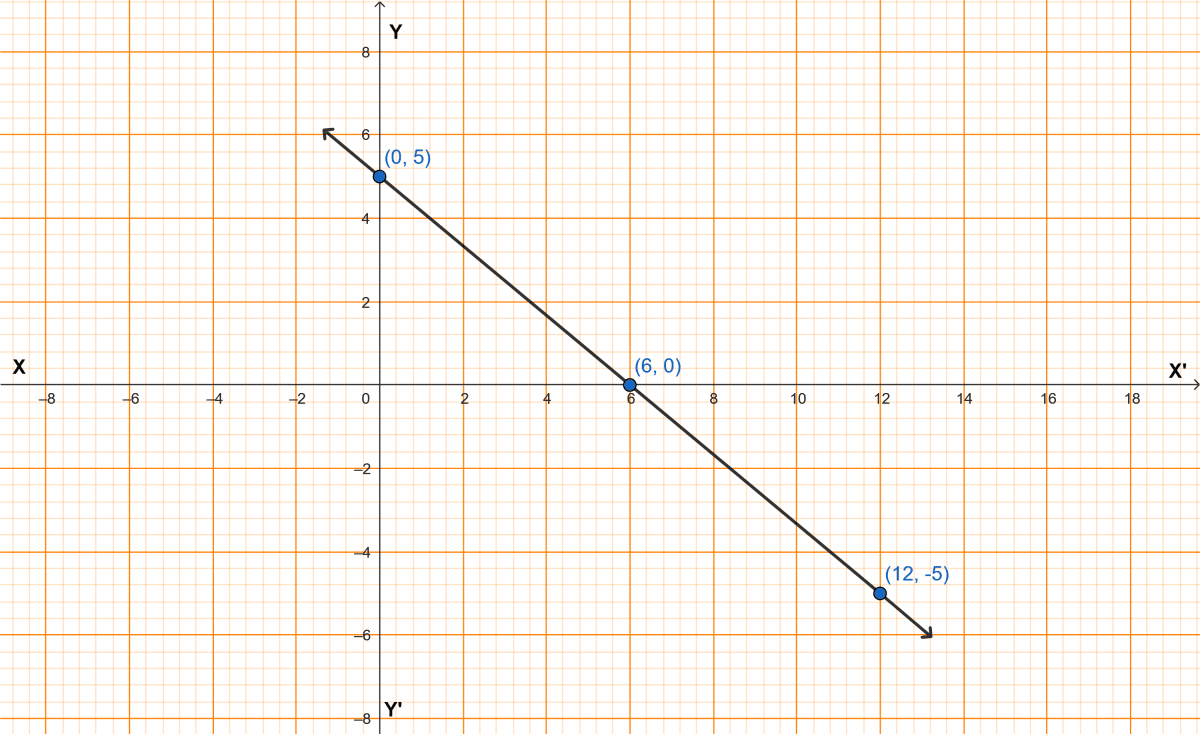
By formula,
Area of triangle =
From graph,
Base = 6 units, Height = 5 units.
Area = sq. units.
Hence, the graph of the given equation is shown in the adjoining figure and area of triangle = 15 sq. units.
Answered By
9 Likes
Related Questions
Draw the graph of 3y = 12 - 2x. Take 2 cm = 1 unit on both axes.
Draw the graph of the following linear equation :
x - 5y - 4 = 0
Draw the graph of 4x - 3y + 12 = 0 and use it to find the area of the triangle formed by the line and co-ordinate axes. Take 2 cm = 1 unit on both axes.
Draw the graph of the equation y = 3x - 4. Find graphically
(i) the value of y when x = -1
(ii) the value of x when y = 5.