Mathematics
Draw a circle of radius 3 cm. Mark a point P at a distance of 5 cm from the center of the circle drawn. Draw two tangents PA and PB to the given circle and measure the length of each tangent.
Answer
Steps of Construction :
Draw a circle with center O and radius 3 cm.
From O, take a point P such that OP = 5 cm.
Draw a perpendicular bisector of OP which intersects OP at M.
With center M and radius OM, draw a circle which intersects the circle with center O at A and B.
Join AP and BP. Measure AP and BP.
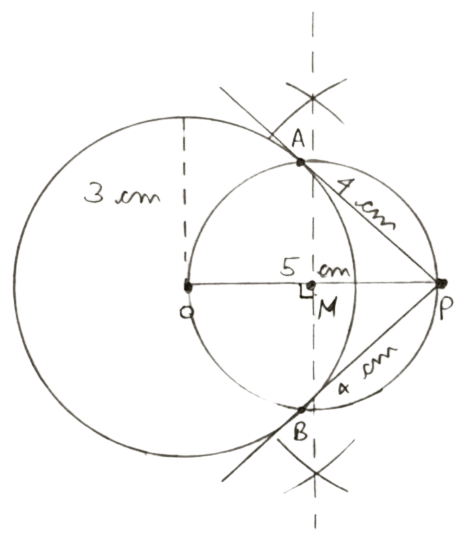
Hence, AP and BP are required tangents.
On measuring,
AP = BP = 4 cm.
Hence, length of each tangent = 4 cm.
Related Questions
Using ruler and compasses only, draw an equilateral triangle of side 4.5 cm and draw its circumscribed circle. Measure the radius of the circle.
ABC is a triangle. In order to draw a tangent PQ to the circle at point A, the angle BAQ is drawn equal to :
∠BAC
∠BCA
∠ABC
∠PAC
Draw a circle of radius 5 cm. Draw two tangents to this circle so that the angle between tangents is 45°.
ABC is an isosceles triangle with AB = AC. Circles are drawn with AB and AC as diameters. The two circles intersect each other at vertex A and a point P which lies in side BC, ∠APB is :
60°
75°
90°
120°