Mathematics
Draw a circle of radius 3 cm. Mark a point P at a distance of 5 cm from the center of the circle drawn. Draw two tangents PA and PB to the given circle and measure the length of each tangent.
Constructions
32 Likes
Answer
Steps of Construction :
Draw a circle with center O and radius 3 cm.
From O, take a point P such that OP = 5 cm.
Draw a perpendicular bisector of OP which intersects OP at M.
With center M and radius OM, draw a circle which intersects the circle with center O at A and B.
Join AP and BP. Measure AP and BP.
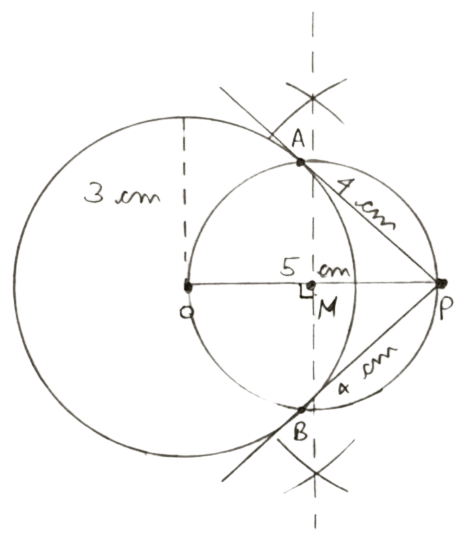
Hence, AP and BP are required tangents.
On measuring,
AP = BP = 4 cm.
Hence, length of each tangent = 4 cm.
Answered By
23 Likes
Related Questions
In ΔABC, PQ is perpendicular bisector of side AB and PR is perpendicular bisector of side BC.
Statement (1): Perpendicular bisector of side AC will pass through point P.
Statement (2): Perpendicular bisectors of sides of a triangle are concurrent.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Pentagon ABCDE is inscribed in a circle with center O.
Statement (1): ∠AOB =
Statement (2): If pentagon is regular, ∠AOB =
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Draw a circle of radius 5 cm. Draw two tangents to this circle so that the angle between tangents is 45°.
Using ruler and compasses only, draw an equilateral triangle of side 4.5 cm and draw its circumscribed circle. Measure the radius of the circle.