Mathematics
ABC is a triangle. In order to draw a tangent PQ to the circle at point A, the angle BAQ is drawn equal to :
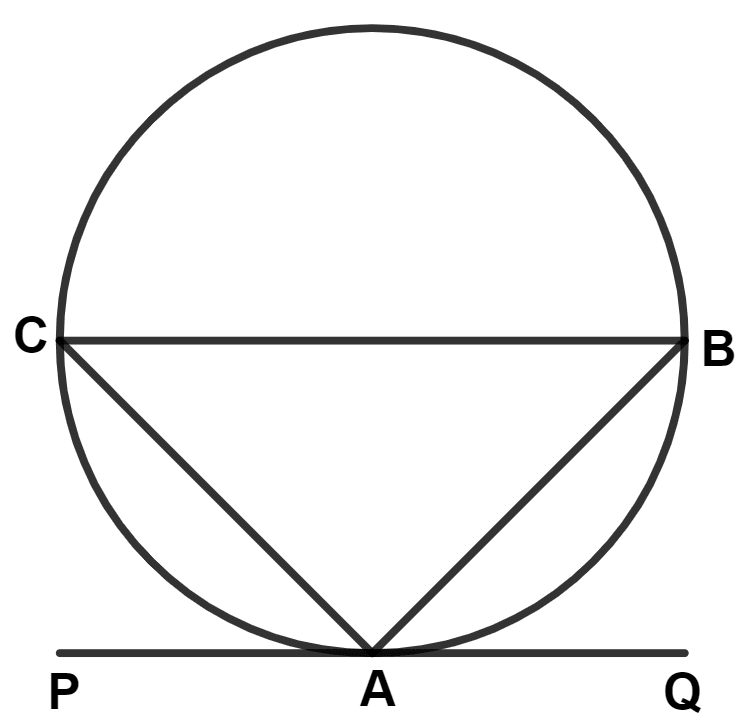
∠BAC
∠BCA
∠ABC
∠PAC
Constructions
3 Likes
Answer
We know that,
The angle between a tangent and a chord through the point of contact is equal to an angle in the alternate segment.
∴ ∠BAQ = ∠BCA.
Hence, Option 2 is the correct option.
Answered By
2 Likes
Related Questions
A regular eight-sided polygon ABCDEF is drawn about a circle with center O, the angle DOE is :
60°
80°
45°
90°
The angle between two radii of a circle is 60°. The angle between their corresponding tangents is :
60°
90°
120°
150°
ABC is an isosceles triangle with AB = AC. Circles are drawn with AB and AC as diameters. The two circles intersect each other at vertex A and a point P which lies in side BC, ∠APB is :
60°
75°
90°
120°
Draw a circle of radius 3 cm. Mark a point P at a distance of 5 cm from the center of the circle drawn. Draw two tangents PA and PB to the given circle and measure the length of each tangent.