Mathematics
Describe :
(i) The locus of points at distances less than 3 cm from a given point.
(ii) The locus of points at distances greater than 4 cm from a given point.
(iii) The locus of points at distances less than or equal to 2.5 cm from a given point.
(iv) The locus of points at distances greater than or equal to 35 mm from a given point.
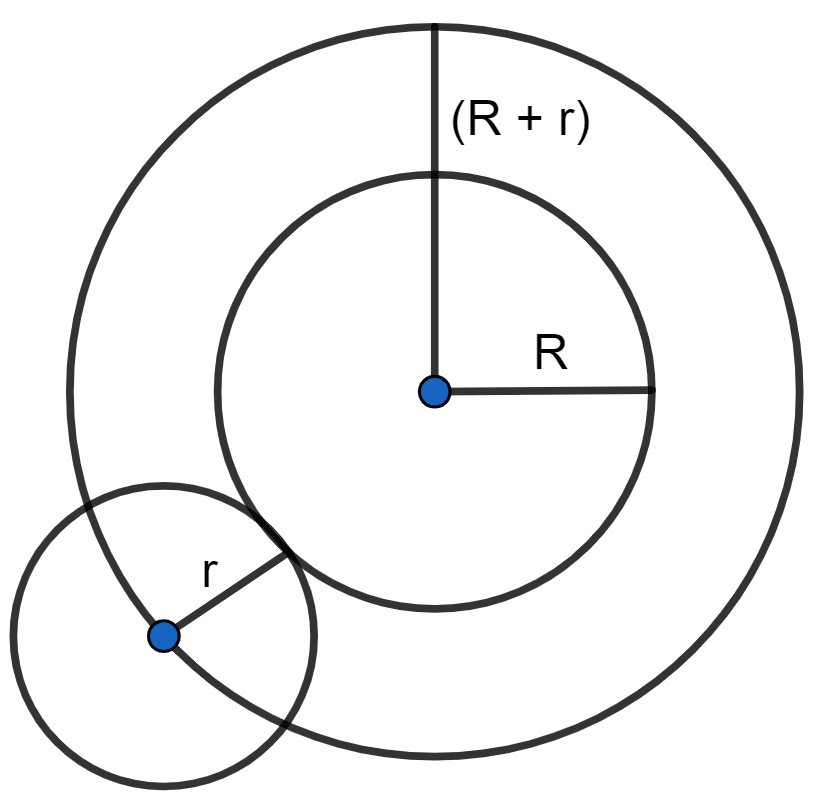
(v) The locus of the center of a given circle which rolls around the outside of a second circle and is always touching it.
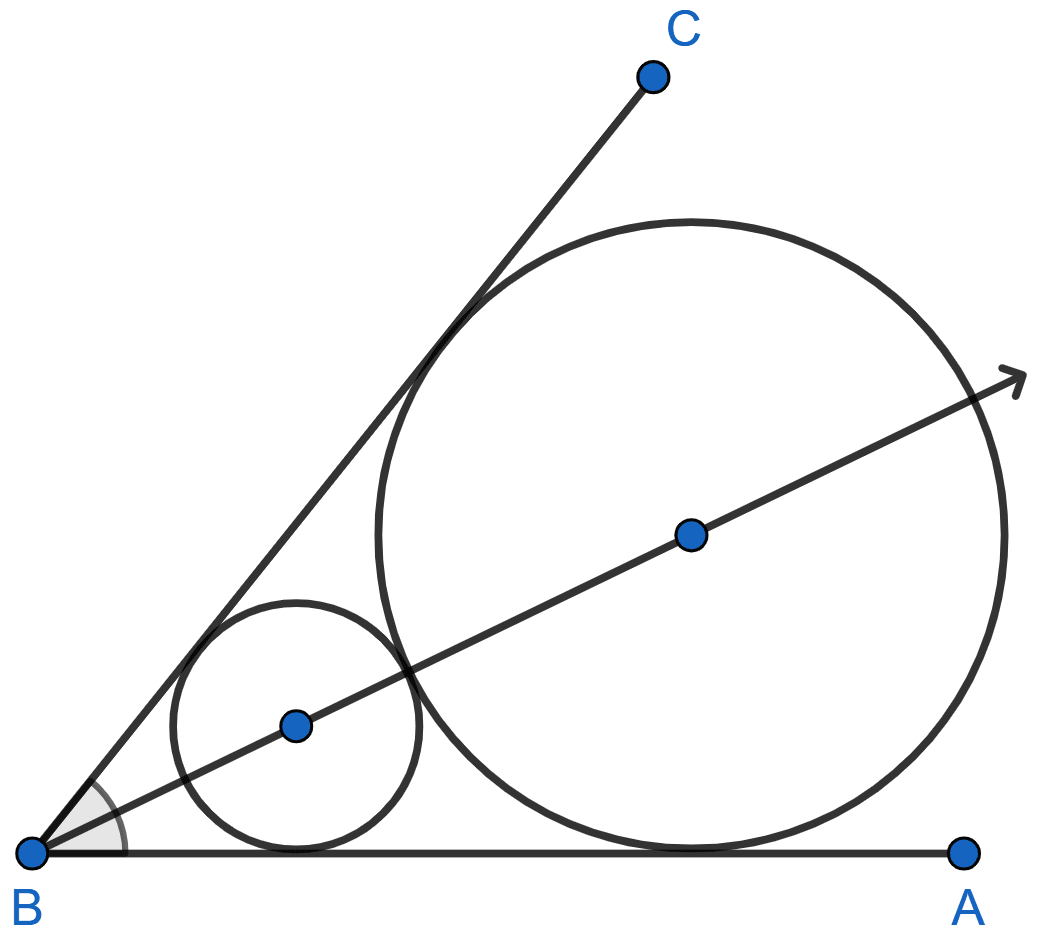
(vi) The locus of the centers of all circles that are tangent to both the arms of a given angle.
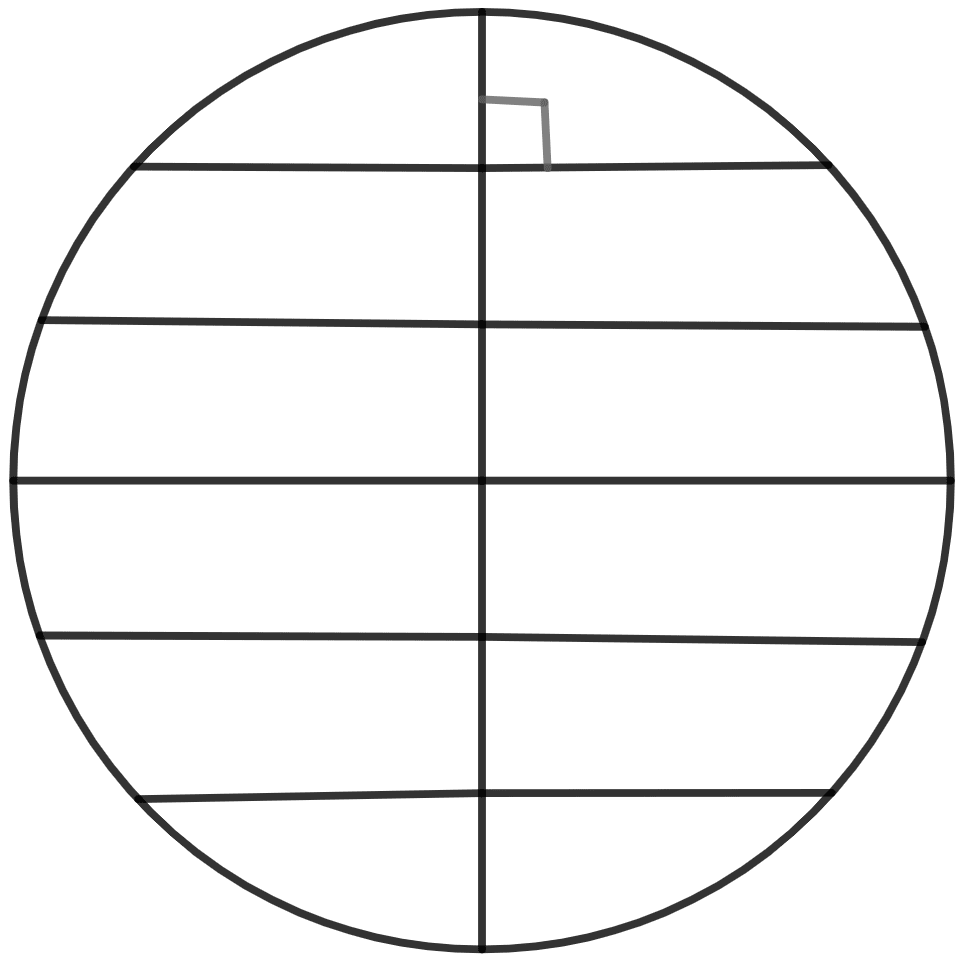
(vii) The locus of the mid-points of all chords parallel to a given chord of a circle.
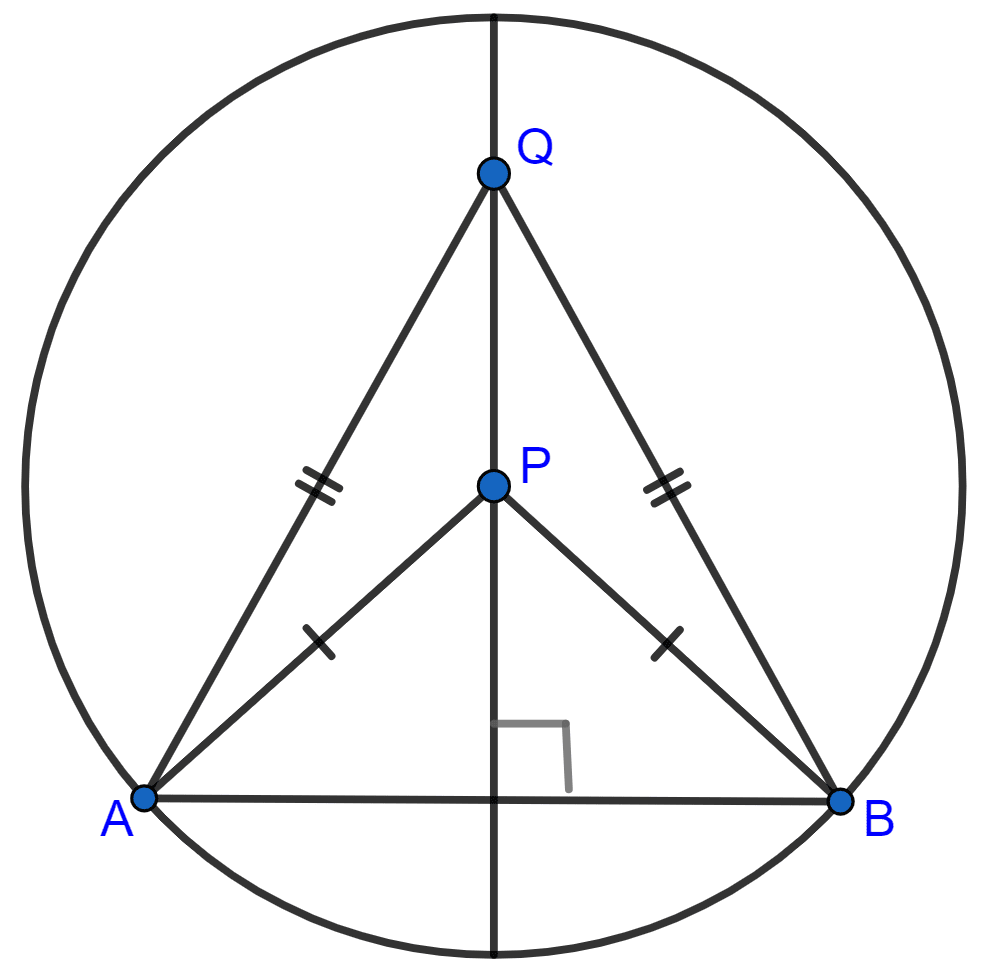
(viii) The locus of points within a circle that are equidistant from the end points of a given chord.
Locus
3 Likes
Answer
(i) The locus is the space inside the circumference of the circle with the given point as centre and radius equal to 3 cm.
(ii) The locus is the space outside the circumference of the circle with the given point as centre and radius equal to 4 cm.
(iii) The locus is the space inside and on the circumference of the circle with the given point as centre and radius equal to 2.5 cm.
(iv) The locus is the space outside and on the circumference of the circle with the given point as centre and radius equal to 35 mm.
(v) The locus is the circumference of the circle concentric with the second circle whose radius is equal to the sum of the radii of the two given circles.
(vi) The locus of the centers of all circles that are tangent to both the arms of a given angle is the bisector of that angle.
(vii) The locus of the mid-points of all chords parallel to a given chord of a circle is the diameter perpendicular to the given chords.
(viii) The locus of points within a circle that are equidistant from the end points of a given chord is the diameter which is perpendicular bisector of the given chord.
Answered By
3 Likes
Related Questions
Describe the locus of a point P, so that :
AB2 = AP2 + BP2,
where A and B are two fixed points.
Describe the locus of a point in rhombus ABCD, so that it is equidistant from
(i) AB and BC.
(ii) B and D.
In the given figure, obtain all the points equidistant from lines m and n; and 2.5 cm from O.

Sketch and describe the locus of the vertices of all triangles with a given base and a given altitude.