Mathematics
D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Prove that the points B, C, E and D are concyclic.
Circles
9 Likes
Answer
Join DE.
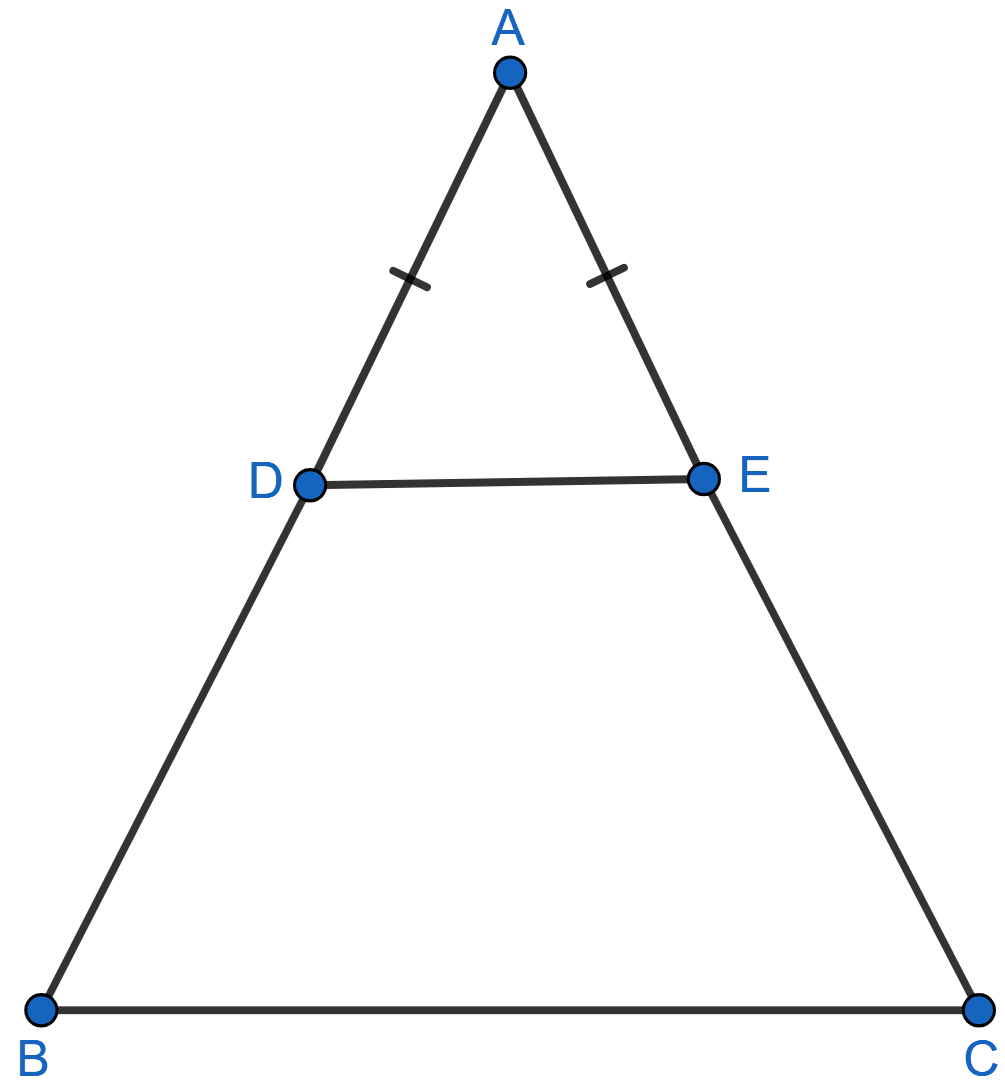
In ∆ABC,
AB = AC = x (let) [Given]
So, ∠B = ∠C [Angles opposite to equal sides are equal]
Similarly,
In ∆ADE,
AD = AE = y (let) [Given]
So, ∠ADE = ∠AED [Angles opposite to equal sides are equal]
Now, in ∆ABC we have
.
Hence, DE || BC [By converse of BPT]
So,
⇒ ∠ADE = ∠B [Corresponding angles are equal]
⇒ (180° - ∠EDB) = ∠B
⇒ ∠B + ∠EDB = 180°
∠B = ∠C [Proved above]
So,
⇒ ∠C + ∠EDB = 180°
Thus, opposite angles are supplementary.
Similarly,
⇒ ∠B + ∠CED = 180°
Since, sum of opposite angles of cyclic quadrilateral = 180°.
Hence, proved that B, C, E and D are concyclic.
Answered By
7 Likes
Related Questions
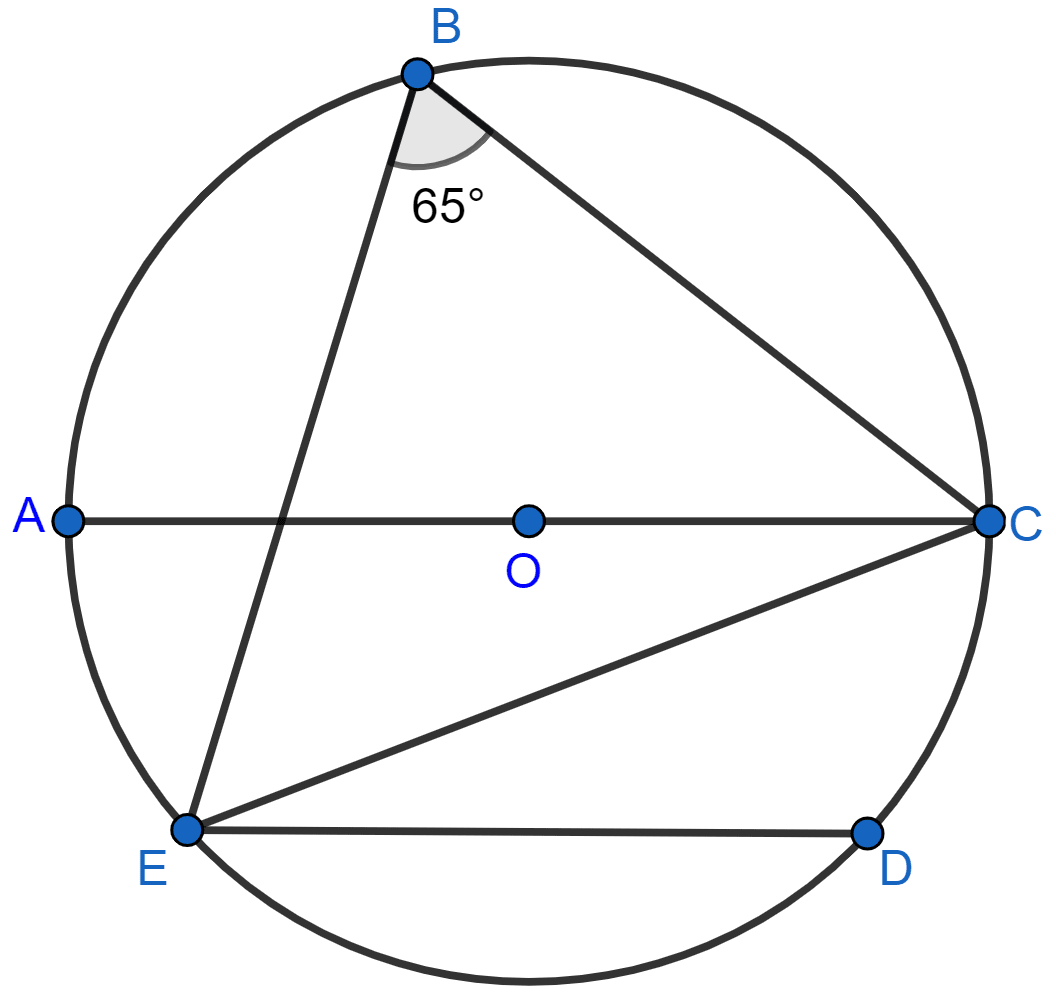
In the given figure, chord ED is parallel to diameter AC of the circle. Given ∠CBE = 65°, calculate ∠DEC.
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate :
(i) ∠BDC
(ii) ∠BEC
(iii) ∠BAC
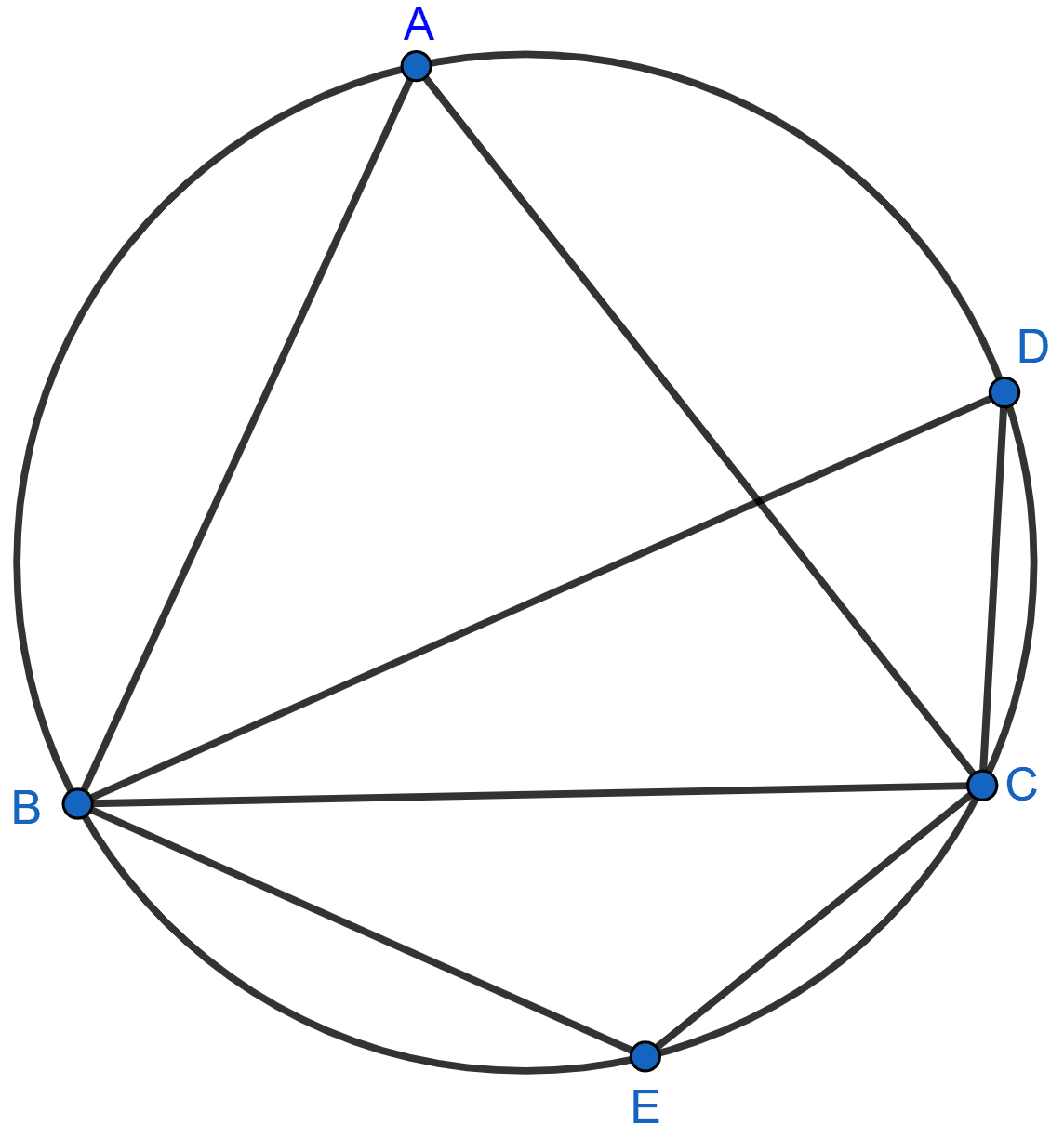
In the given figure, ABCD is a cyclic quadrilateral. AF is drawn parallel to CB and DA is produced to point E. If ∠ADC = 92°, ∠FAE = 20°; determine ∠BCD. Given reason in support of your answer.

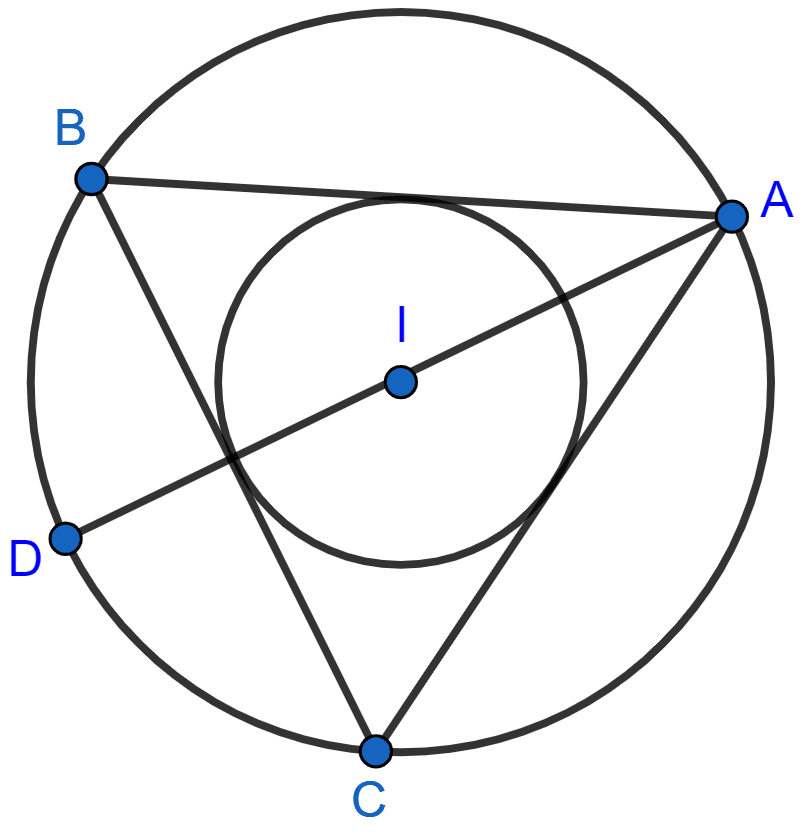
If I is the incentre of triangle ABC and AI when produced meets the circumcircle of triangle ABC in point D. If ∠BAC = 66° and ∠ABC = 80°. Calculate :
(i) ∠DBC,
(ii) ∠IBC,
(iii) ∠BIC.