Mathematics
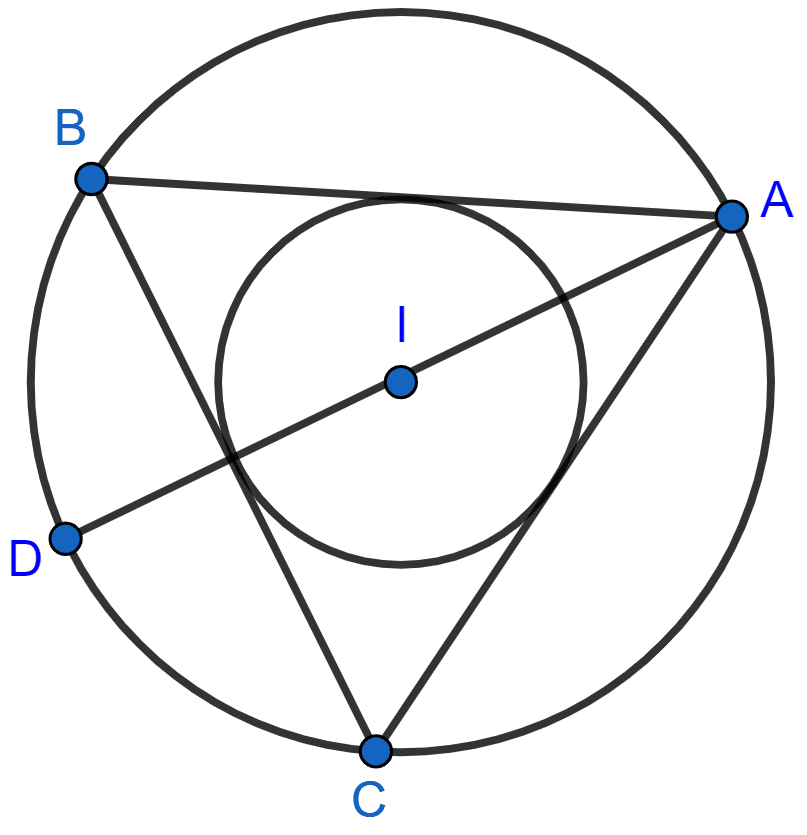
If I is the incentre of triangle ABC and AI when produced meets the circumcircle of triangle ABC in point D. If ∠BAC = 66° and ∠ABC = 80°. Calculate :
(i) ∠DBC,
(ii) ∠IBC,
(iii) ∠BIC.
Circles
13 Likes
Answer
Join DB and DC, IB and IC.
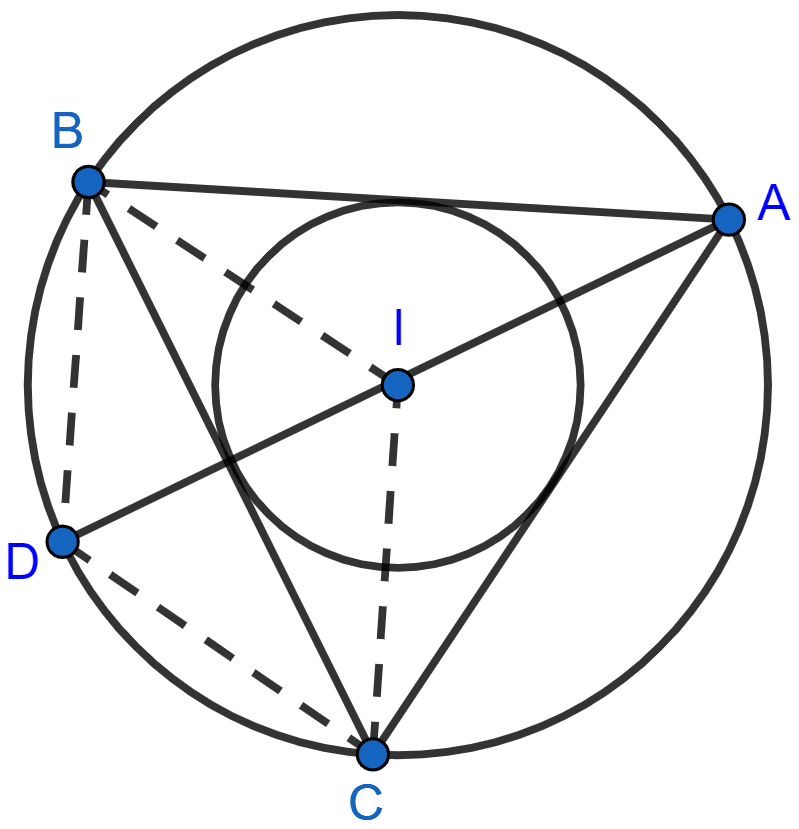
(i) From figure,
∠DAC = ∠BAC [As I is the incenter]
∠DAC = x 66° = 33°.
As angle in same segment are equal.
∴ ∠DBC = ∠DAC = 33°.
Hence, ∠DBC = 33°.
(ii) Since, I is the incentre of ∆ABC, IB bisects ∠ABC.
∴ ∠IBC = ∠ABC
= = 40°.
Hence, ∠IBC = 40°.
(iii) In ∆ABC,
⇒ ∠ACB + ∠ABC + ∠BAC = 180° [By angle sum property]
⇒ ∠ACB = 180° - ∠ABC - ∠BAC
⇒ ∠ACB = 180° - 80° - 66°
⇒ ∠ACB = 180° - 146°
⇒ ∠ACB = 34°.
As I is incenter so, IC bisects ∠C
∴ ∠ICB = ∠ACB = = 17°.
In ∆IBC
⇒ ∠IBC + ∠ICB + ∠BIC = 180° [By angle sum property of triangle]
⇒ 40° + 17° + ∠BIC = 180°
⇒ 57° + ∠BIC = 180°
⇒ ∠BIC = 180° - 57° = 123°.
Hence, ∠BIC = 123°.
Answered By
9 Likes
Related Questions
D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Prove that the points B, C, E and D are concyclic.
In the given figure, ABCD is a cyclic quadrilateral. AF is drawn parallel to CB and DA is produced to point E. If ∠ADC = 92°, ∠FAE = 20°; determine ∠BCD. Given reason in support of your answer.

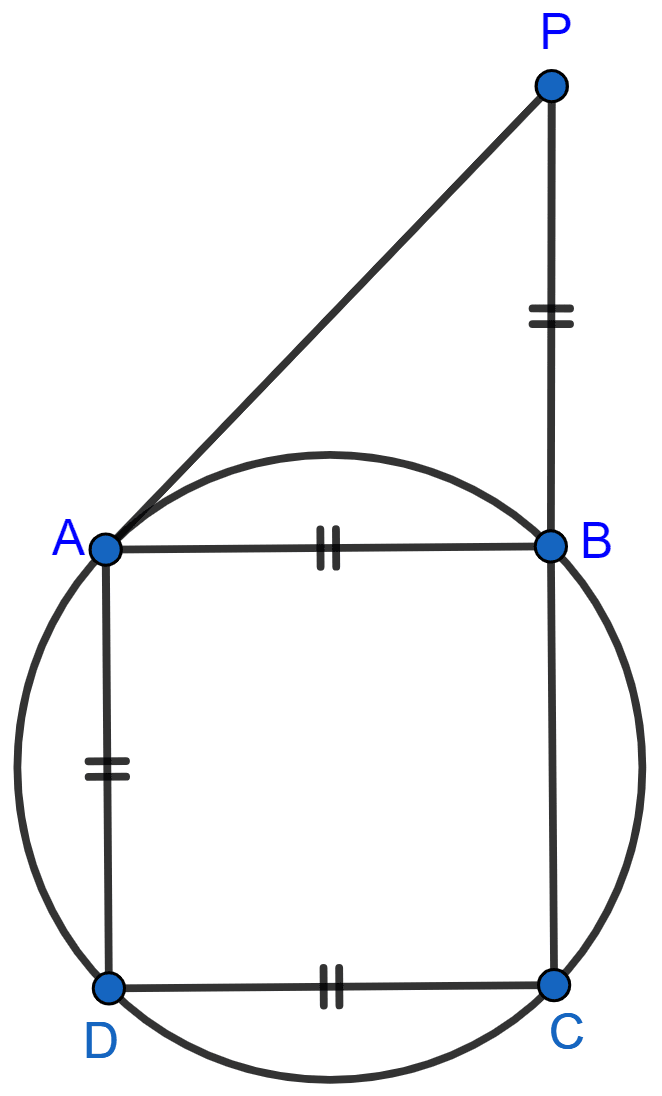
In the given figure, AB = AD = DC = PB and ∠DBC = x°. Determine, in terms of x :
(i) ∠ABD, (ii) ∠APB.
Hence or otherwise, prove that AP is parallel to DB.
In the given figure; ABC, AEQ and CEP are straight lines. Show that ∠APE and ∠CQE are supplementary.