Mathematics
Construct a triangle ABC such that AB = 7 cm, BC = 6 cm and CA = 5 cm.
(a) Draw the locus of the points such that
(i) it is equidistant from BC and BA.
(ii) it is equidistant from points A and B.
(b) Mark P where the loci (i) and (ii) meet, measure and write length of PA.
Answer
We know that,
Locus of the points equidistant from two sides is the angle bisector between two sides.
Locus of the points equidistant from two points is the perpendicular bisector of the line joining two points.
Steps of construction :
Draw a line segment AB = 7 cm.
With A and B as center and radii 5 cm and 6 cm respectively draw arcs intersecting at C.
Join AC and BC.
Draw BD, angle bisector of B.
Draw XY perpendicular bisector of AB.
Mark point P, the intersection point of XY and BD.
Measure AP.
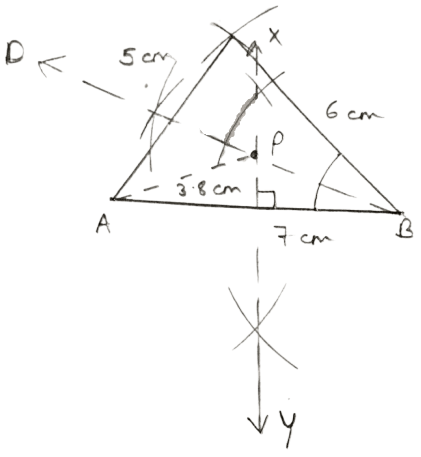
Hence, AP = 3.8 cm.
Related Questions
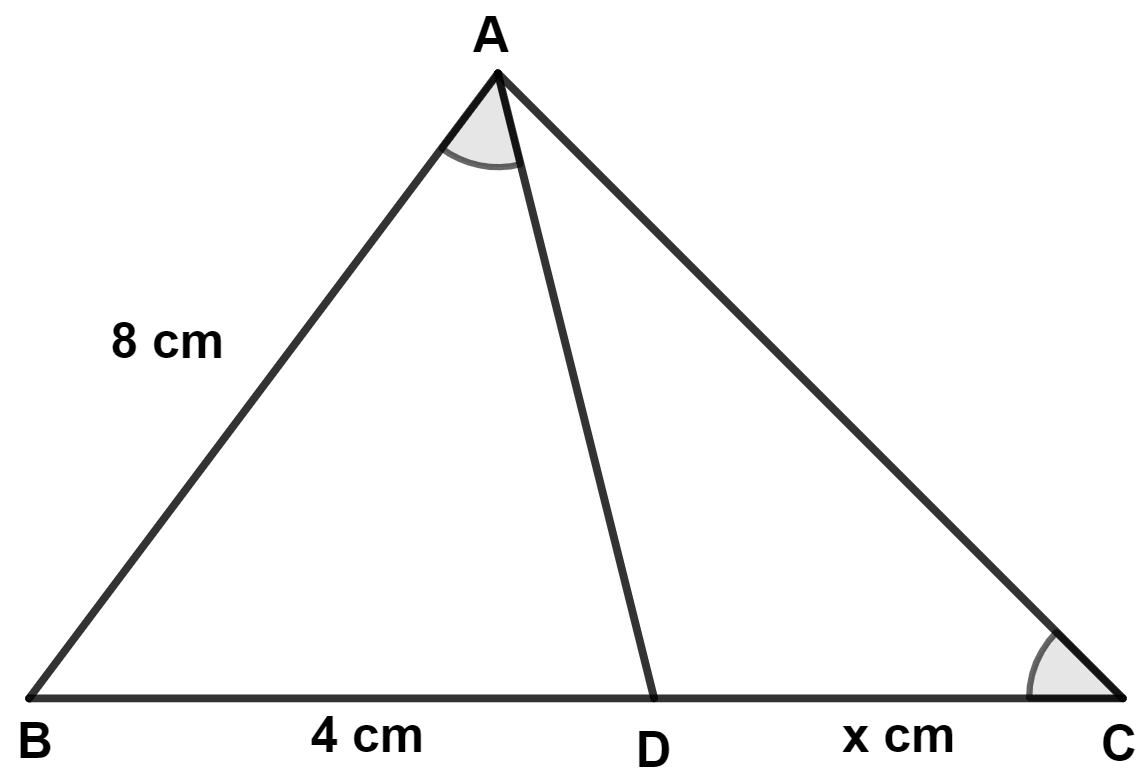
Given a triangle ABC, and D is a point on BC such that BD = 4 cm and DC = x cm. If ∠BAD = ∠C and AB = 8 cm, then,
(a) prove that triangle ABD is similar to triangle CBA.
(b) find the value of 'x'.
In the extract of Survey of India map G43S7, prepared on a scale of 2 cm to 1 km, a child finds the length of the cart track between two settlements is 7.6 cm. Find :
(a) the actual length of the cart track on the ground.
(b) actual area of a grid square, if each has an area of 4 cm2.
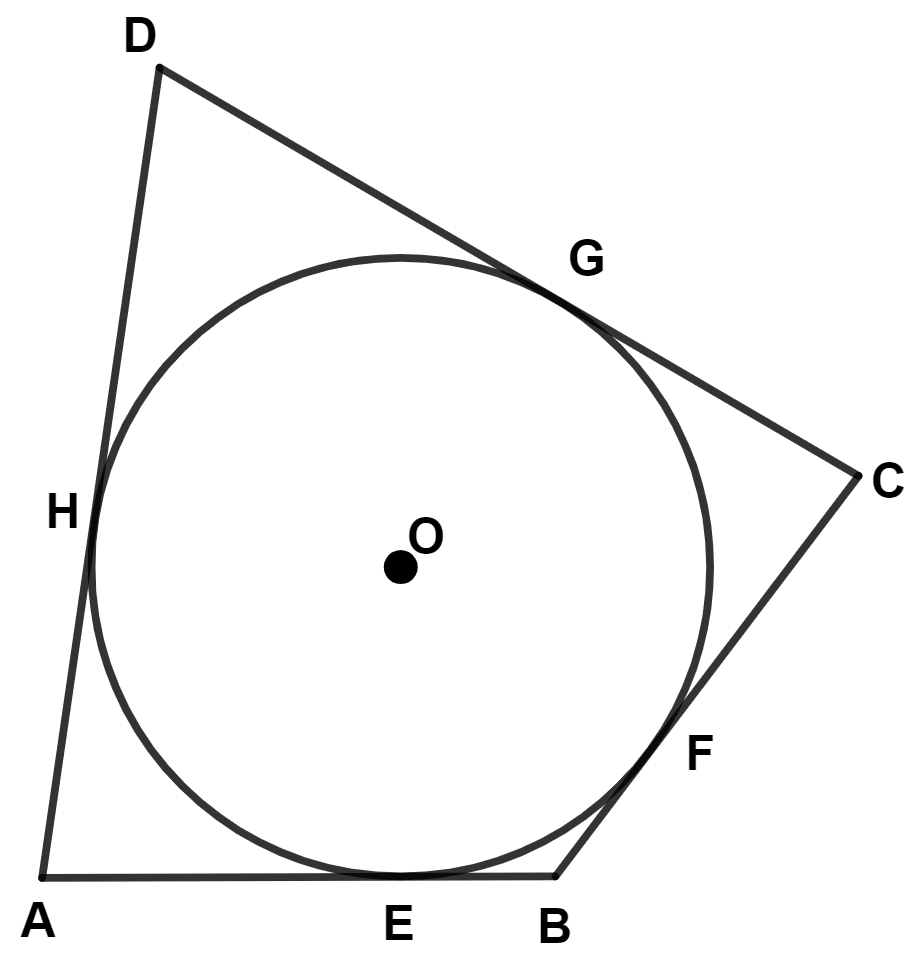
In the given figure O is the centre of the circle. ABCD is a quadrilateral where sides AB, BC, CD and DA touch the circle at E, F, G and H respectively. If AB = 15 cm, BC = 18 cm and AD = 24 cm, find the length of CD.
In the given diagram, ABCDEF is a regular hexagon inscribed in a circle with centre O. PQ is a tangent to the circle at D. Find the value of :
(a) ∠FAG
(b) ∠BCD
(c) ∠PDE