Mathematics
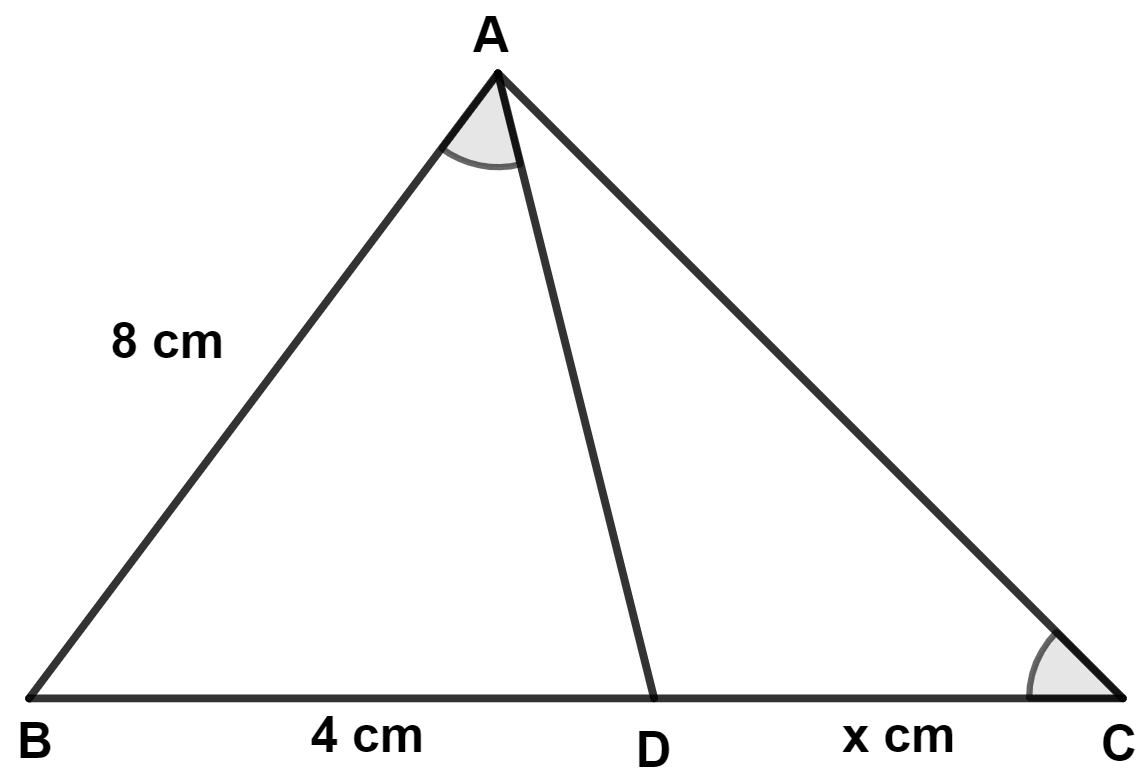
Given a triangle ABC, and D is a point on BC such that BD = 4 cm and DC = x cm. If ∠BAD = ∠C and AB = 8 cm, then,
(a) prove that triangle ABD is similar to triangle CBA.
(b) find the value of 'x'.
Similarity
31 Likes
Answer
(a) In △ ABD and △ CBA,
⇒ ∠ABD = ∠CBA (Common angle)
⇒ ∠BAD = ∠ACB (Given)
∴ △ ABD ~ △ CBA (By A.A. axiom)
Hence, proved that △ ABD ~ △ CBA.
(b) We know that,
Corresponding sides of similar triangle are proportional.
Hence, x = 12 cm.
Answered By
15 Likes
Related Questions
Square ABCD lies in the third quadrant of a XY plane such that its vertex A is at (-3, -1) and the diagonal DB produced is equally inclined to both the axes. The diagonals AC and BD meets at P(-2, -2). Find the :
(a) Slope of BD
(b) equation of AC
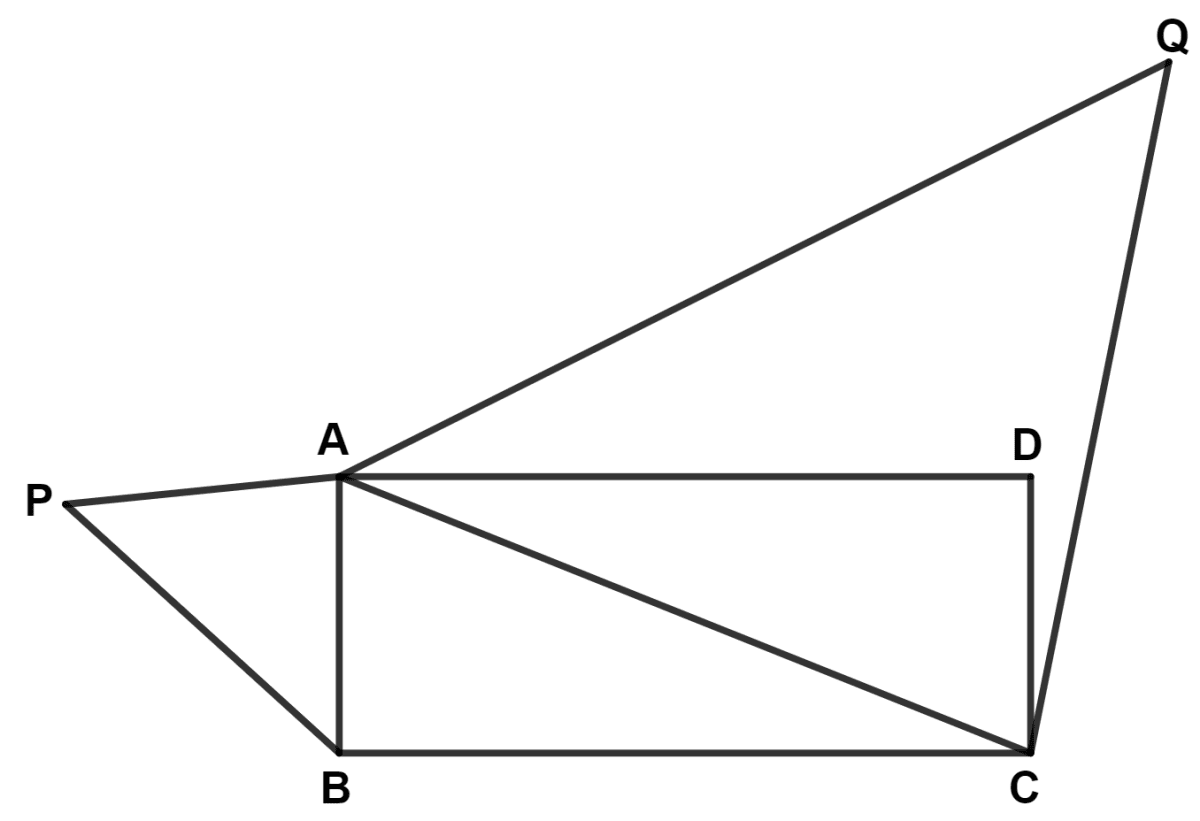
ABCD is a rectangle where side BC is twice side AB. If △ACQ ~ △BAP, find area of △BAP : area of △ACQ.
In the extract of Survey of India map G43S7, prepared on a scale of 2 cm to 1 km, a child finds the length of the cart track between two settlements is 7.6 cm. Find :
(a) the actual length of the cart track on the ground.
(b) actual area of a grid square, if each has an area of 4 cm2.
Construct a triangle ABC such that AB = 7 cm, BC = 6 cm and CA = 5 cm.
(a) Draw the locus of the points such that
(i) it is equidistant from BC and BA.
(ii) it is equidistant from points A and B.
(b) Mark P where the loci (i) and (ii) meet, measure and write length of PA.