JOIN NOW

Mathematics

As shown in the figure, the tangent at point C of the circle and diameter AB when produced intersect at point P. If angle PCA = 110°, find the angle CBA.

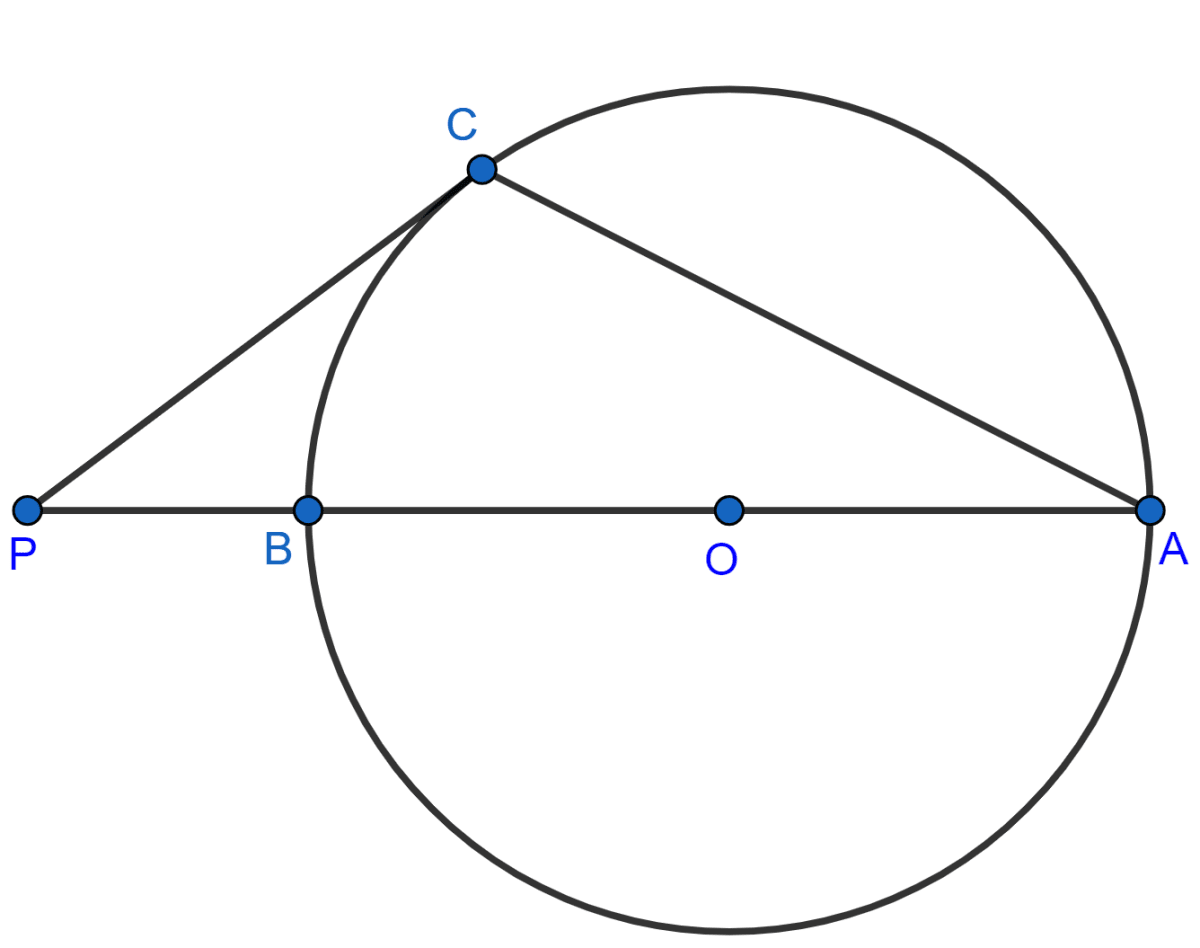
As shown in the figure, the tangent at point C of the circle and diameter AB when produced intersect at point P. If angle PCA = 110°, find the angle CBA. Model Paper 1, Concise Mathematics Solutions ICSE Class 10.

Circles

2 Likes

Answer

Given,

∠PCA = 110°

PC is the tangent to the circle whose centre is O.

Construction :

  1. Join CO.
  2. Join CB.
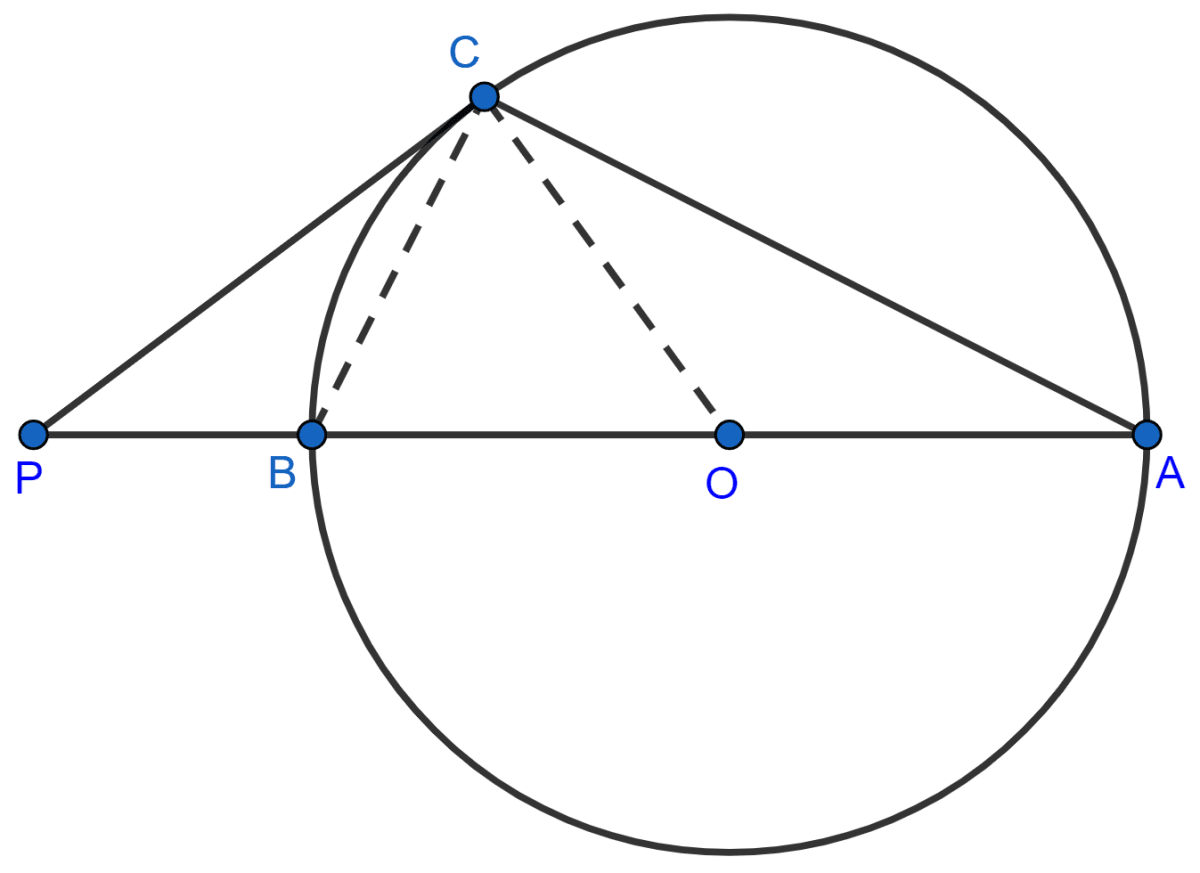
As shown in the figure, the tangent at point C of the circle and diameter AB when produced intersect at point P. If angle PCA = 110°, find the angle CBA. Model Paper 1, Concise Mathematics Solutions ICSE Class 10.

∠BCA = 90° [Since angle in a semi circle is 90°]

∠PCO = 90° [Since radius ⊥ tangent]

From the figure we have,

⇒ ∠PCA = ∠PCO + ∠OCA

⇒ 110° = 90° + ∠OCA

⇒ ∠OCA = 110° - 90° = 20°

In Δ AOC,

AO = OC [Radius of same circle]

As, angles opposite to equal sides are equal.

∴ ∠OCA = ∠OAC = 20°

From figure,

∠CAB = ∠OAC = 20°.

In Δ ABC, we have

∠BCA = 90°

∠CAB = 20°

By angle sum property of triangle,

⇒ ∠BCA + ∠CAB + ∠CBA = 180°

⇒ 90° + 20° + ∠CBA = 180°

⇒ ∠CBA = 180° - 90° - 20°

⇒ ∠CBA = 70°

Hence, ∠CBA = 70°.

Answered By

2 Likes

Related Questions