Mathematics
As shown in the figure, the tangent at point C of the circle and diameter AB when produced intersect at point P. If angle PCA = 110°, find the angle CBA.
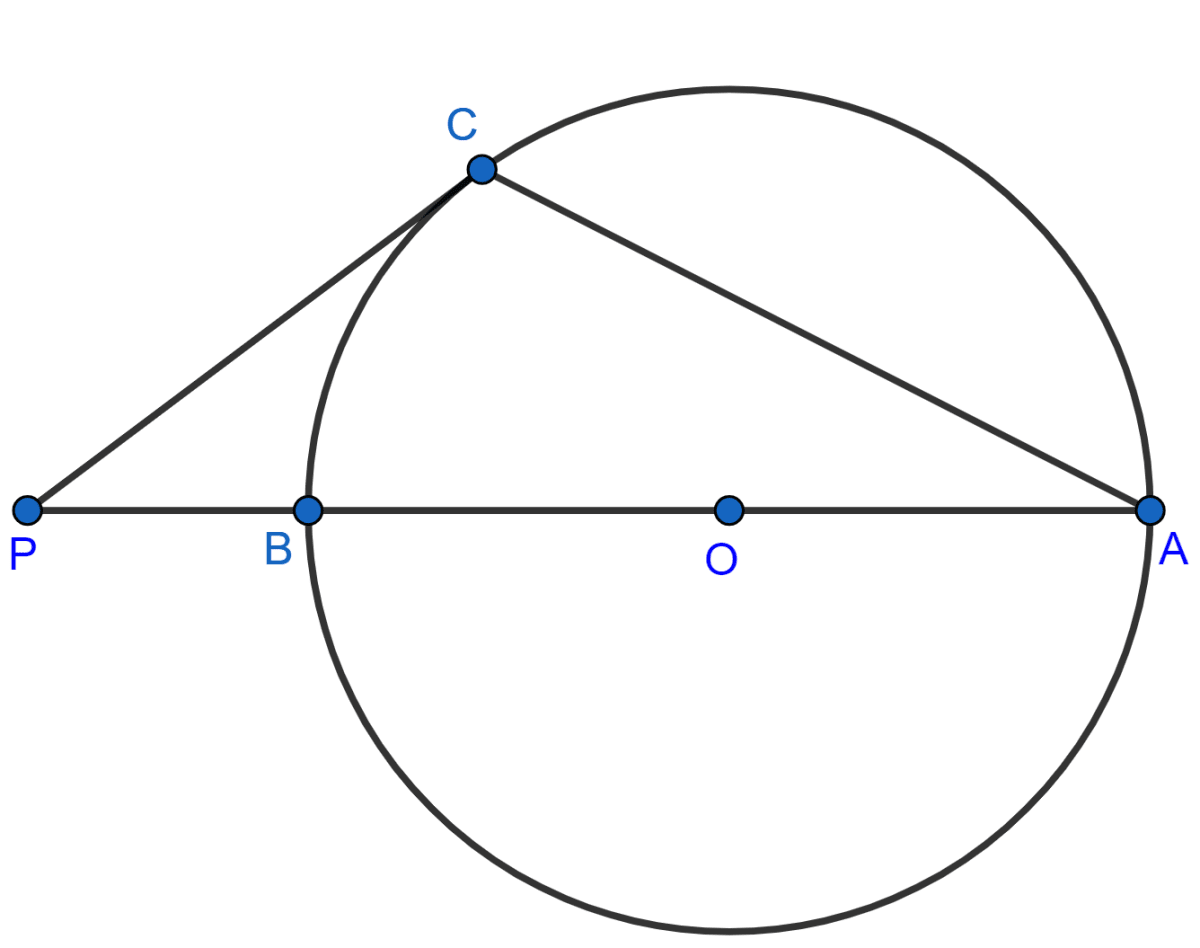
Circles
2 Likes
Answer
Given,
∠PCA = 110°
PC is the tangent to the circle whose centre is O.
Construction :
- Join CO.
- Join CB.
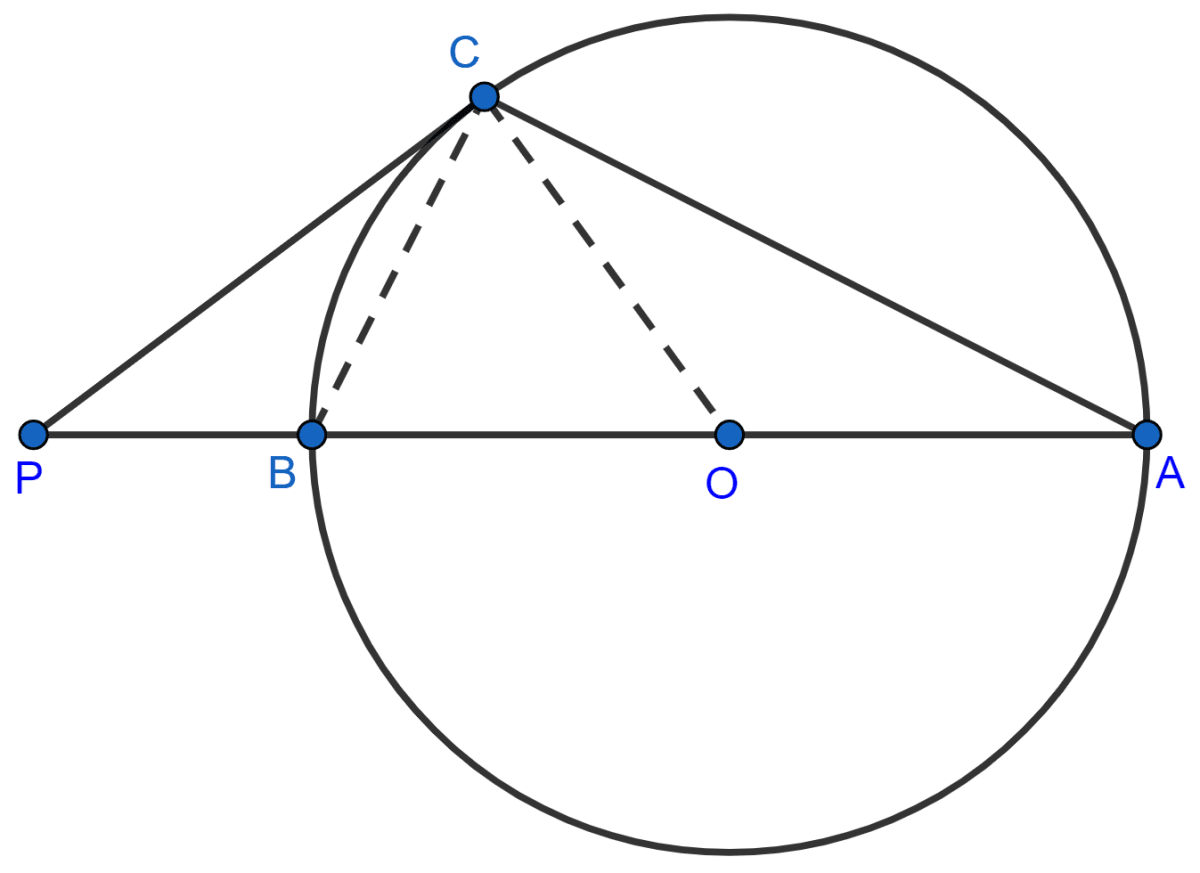
∠BCA = 90° [Since angle in a semi circle is 90°]
∠PCO = 90° [Since radius ⊥ tangent]
From the figure we have,
⇒ ∠PCA = ∠PCO + ∠OCA
⇒ 110° = 90° + ∠OCA
⇒ ∠OCA = 110° - 90° = 20°
In Δ AOC,
AO = OC [Radius of same circle]
As, angles opposite to equal sides are equal.
∴ ∠OCA = ∠OAC = 20°
From figure,
∠CAB = ∠OAC = 20°.
In Δ ABC, we have
∠BCA = 90°
∠CAB = 20°
By angle sum property of triangle,
⇒ ∠BCA + ∠CAB + ∠CBA = 180°
⇒ 90° + 20° + ∠CBA = 180°
⇒ ∠CBA = 180° - 90° - 20°
⇒ ∠CBA = 70°
Hence, ∠CBA = 70°.
Answered By
2 Likes
Related Questions
A and B are two events such that P(A) = 0.56 and P(B) = 0.64, find :
(i) P(not A)
(ii) P(not B)
A largest possible sphere is carved out from a solid wooden cube of side 7 cm. Find :
(i) the volume of sphere
(ii) the percentage of wood wasted in the process.
(Take π = )
Calculate the mean, by step-deviation method, for the frequency distribution given below :
Class-interval Frequency 0-5 6 5-10 14 10-15 30 15-20 48 20-25 32 25-30 16 30-35 10 35-40 4 Solve , x ∈ R. Also represent the solution set on the number line.