KnowledgeBoat Logo

Mathematics

An observer 1.5 m tall is 20.5 meters away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer.

Heights & Distances

17 Likes

Answer

Let CD be an observer of height 1.5 m which is 20.5 m away from a tower AB of height 22 m.

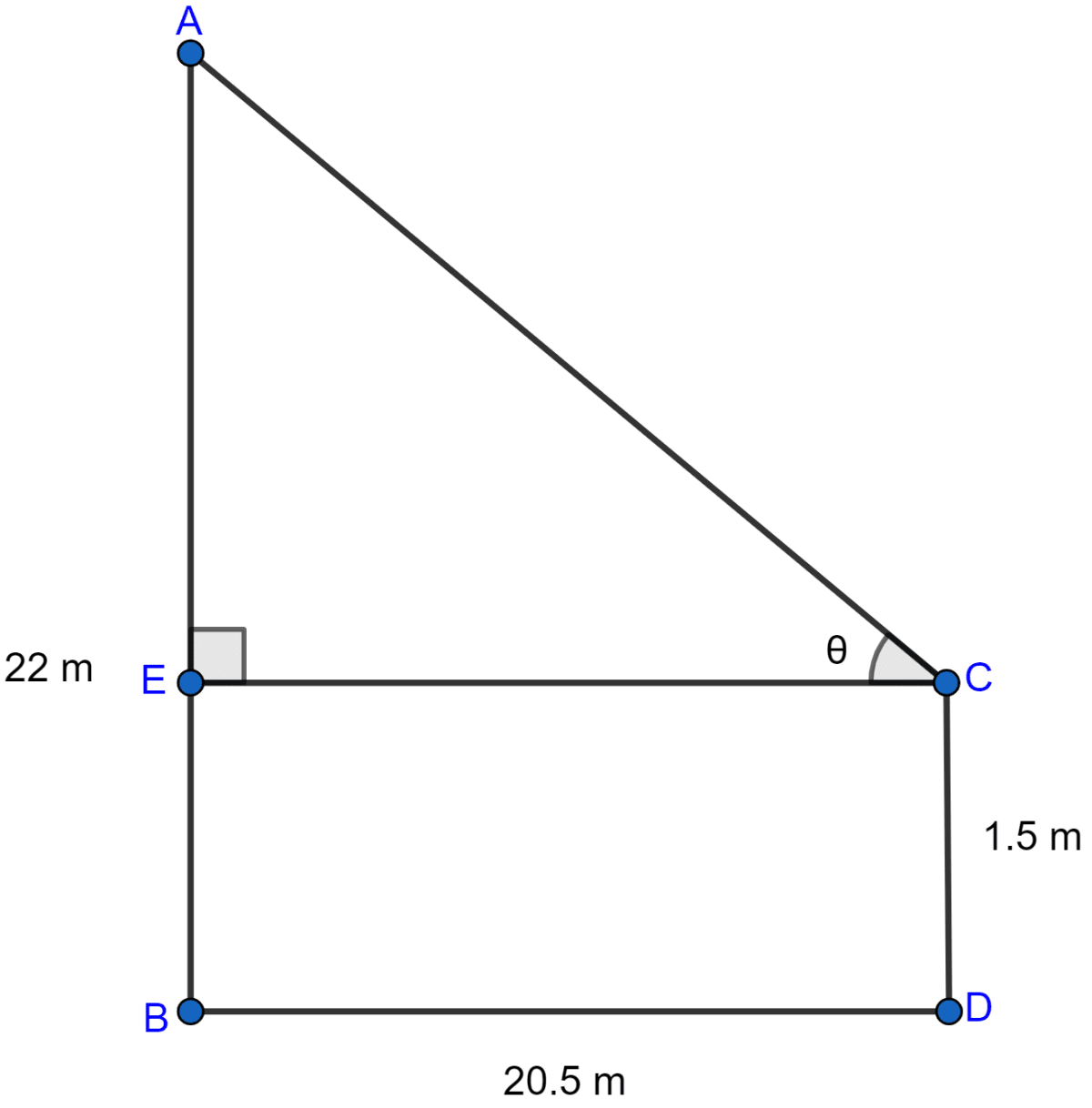
An observer 1.5 m tall is 20.5 meters away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer. Heights and Distances, ML Aggarwal Understanding Mathematics Solutions ICSE Class 10.

CD = 1.5 m and DB = 20.5 m

From C, draw CE ⊥ AB, then CDBE is a rectangle.

AE = AB - BE = AB - CD = 22 - 1.5 = 20.5 m
CE = DB = 20.5 m.

Let angle of elevation be θ,

From right angled △ACE, we get

⇒tan θ=AECE⇒tan θ=20.520.5⇒tan θ=1⇒tan θ=tan 45°∴θ=45°.\Rightarrow \text{tan θ} = \dfrac{AE}{CE} \\[1em] \Rightarrow \text{tan θ} = \dfrac{20.5}{20.5} \\[1em] \Rightarrow \text{tan θ} = 1 \\[1em] \Rightarrow \text{tan θ} = \text{tan 45°} \\[1em] \therefore \text{θ} = 45°.

Hence, the angle of elevation of the top of the tower from the eye of the observer is 45°.

Answered By

11 Likes

Related Questions