In the adjoining figure, the angle of elevation from a point P of the top of a tower QR, 50 m high is 60° and that of the tower PT from a point Q is 30°. Find the height of the tower PT, correct to the nearest metre.

Let height of tower PT be h meters.

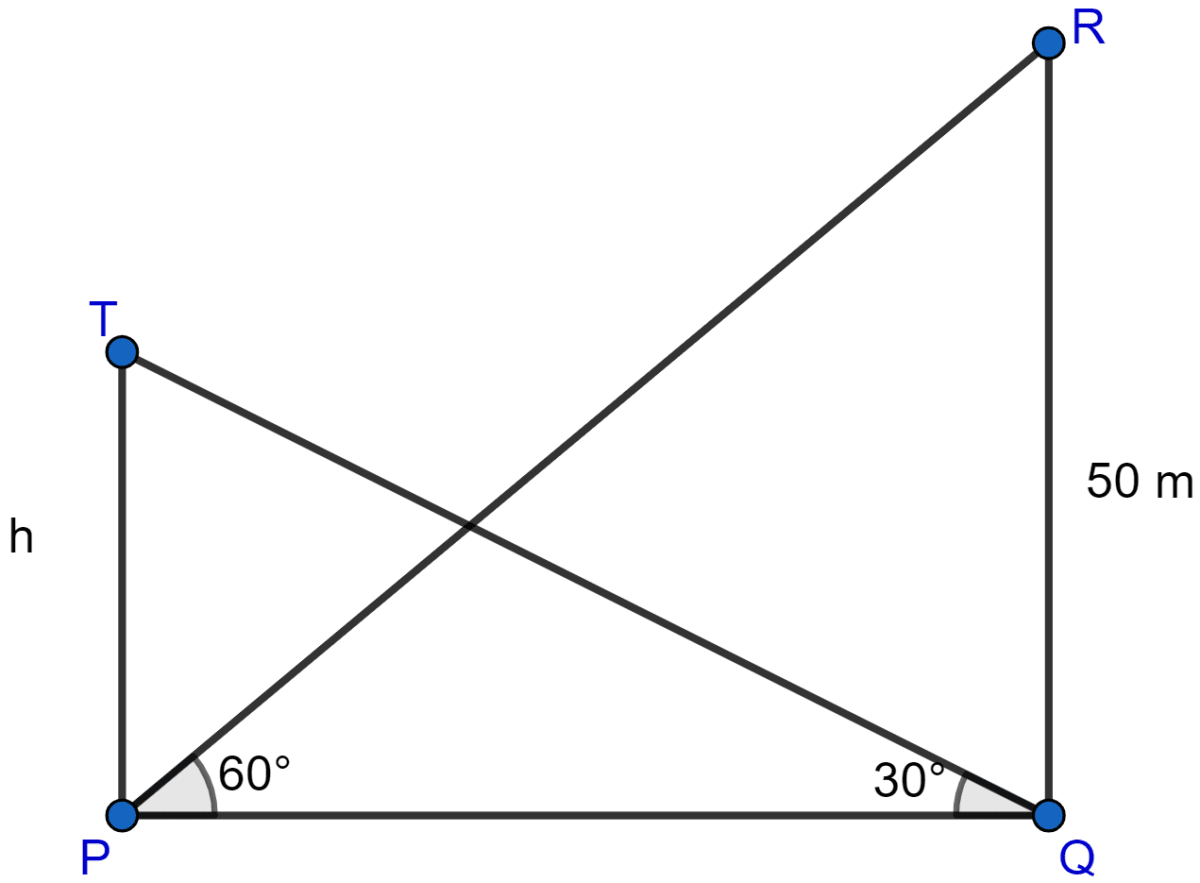
Considering right angled △PQR, we get

$\Rightarrow \text{tan 60°} = \dfrac{QR}{PQ} \\[1em] \Rightarrow \text{tan 60°} = \dfrac{50}{PQ} \\[1em] \Rightarrow \sqrt{3} = \dfrac{50}{PQ} \\[1em] \Rightarrow PQ = \dfrac{50}{\sqrt{3}} \\[1em]$

Now considering right angled △PQT, we get

$\Rightarrow \text{tan 30°} = \dfrac{h}{PQ} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{h}{\dfrac{50}{\sqrt{3}}} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{\sqrt{3} \times h}{50} \\[1em] \Rightarrow h = \dfrac{50}{\sqrt{3} \times \sqrt{3}} \\[1em] \Rightarrow h = \dfrac{50}{3} \\[1em] \Rightarrow h = 16.7.$

On correcting to nearest meter, h = 17 m.

Hence, the height of the tower PT = 17 m.