Mathematics
ABCD is a trapezium in which AB || CD and AD = BC. Show that
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) Δ ABC ≅ Δ BAD
(iv) diagonal AC = diagonal BD
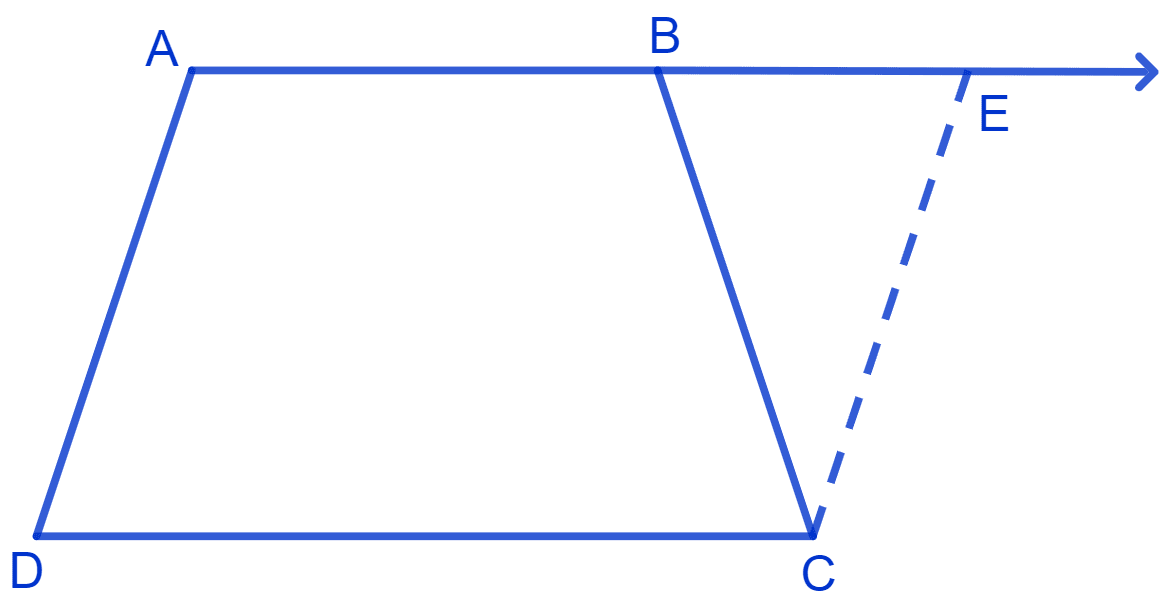
Answer
Steps of construction :
Extend AB.
Draw a line through C parallel to DA intersecting AB produced at E.
Given :
ABCD is a trapezium, AB || CD and AD = BC
By construction,
AD || CE
and
AE || DC.
In AECD, both pair of opposite sides are parallel, hence, AECD is a parallelogram
(i) From figure,
AD = CE (Opposite sides of parallelogram are equal)
As,
AD = BC
∴ BC = CE
We know that,
Angles opposite to equal sides in a triangle are also equal.
⇒ ∠CEB = ∠CBE ………(1)
Consider, parallel lines AD and CE where AE is the transversal.
We know that,
Sum of co-interior angles = 180°
⇒ ∠BAD + ∠CEB = 180°
⇒ ∠BAD + ∠CBE = 180° [From equation (1)] ….. (2)
From figure,
⇒ ∠ABC + ∠CBE = 180° (Linear pairs) ……. (3)
From equations (2) and (3), we get :
⇒ ∠BAD + ∠CBE = ∠ABC + ∠CBE
⇒ ∠BAD = ∠ABC.
∴ ∠A = ∠B
Hence, proved that ∠A = ∠B.
(ii) From figure,
AB || CD
We know that,
Sum of co-interior angles equal to 180°.
⇒ ∠A + ∠D = 180° ………(4)
⇒ ∠C + ∠B = 180° ………(5)
From equation (4) and (5), we get :
⇒ ∠A + ∠D = ∠C + ∠B
Since, ∠A = ∠B
We can say that,
⇒ ∠D = ∠C
Hence, proved that ∠C = ∠D.
(iii) Join AC and BD.
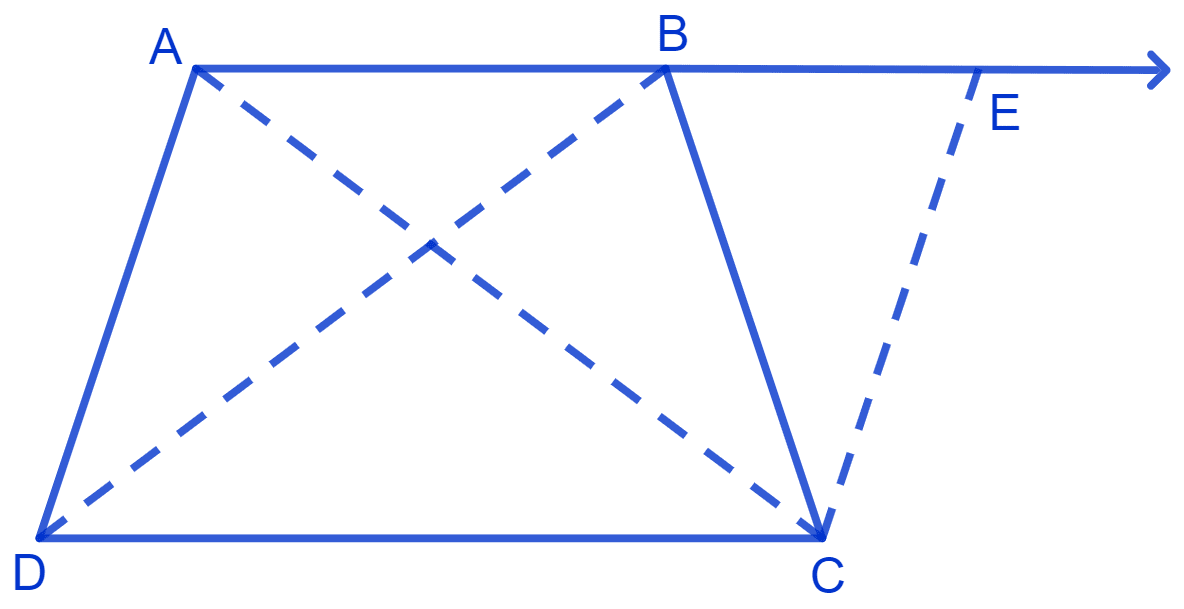
In ∆ ABC and ∆ BAD,
⇒ AB = BA (Common side)
⇒ BC = AD (Given)
⇒ ∠B = ∠A (above)
∴ ∆ ABC ≅ ∆ BAD (By S.A.S. congruence rule)
Hence, proved that Δ ABC ≅ Δ BAD.
(iv) Since ∆ ABC ≅ ∆ BAD,
We know that,
Corresponding parts of congruent triangles are equal.
⇒ AC = BD (By C.P.C.T.)
Hence, proved that diagonal AC = diagonal BD.
Related Questions
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ see Fig. Show that:
(i) Δ APD ≅ Δ CQB
(ii) AP = CQ
(iii) Δ AQB ≅ Δ CPD
(iv) AQ = CP
(v) APCQ is a parallelogram

ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD. Show that
(i) Δ APB ≅ Δ CQD
(ii) AP = CQ
ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.