Mathematics
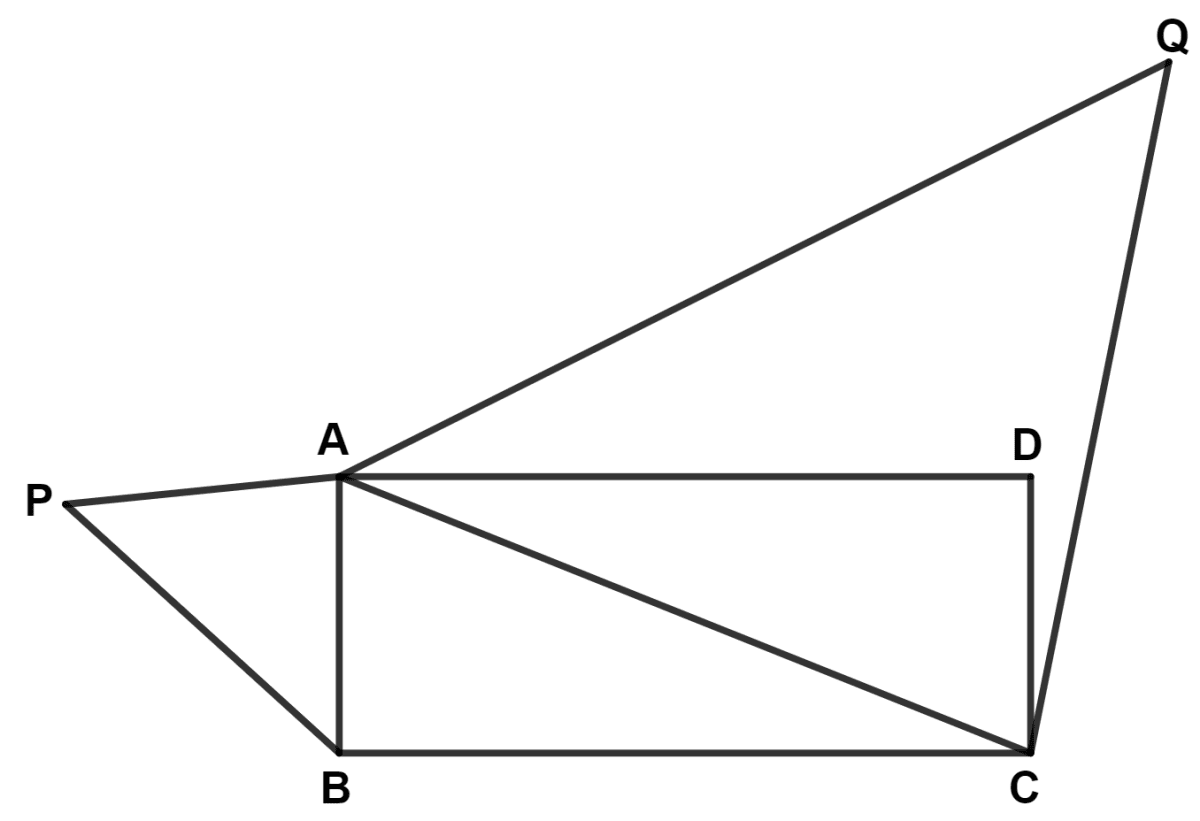
ABCD is a rectangle where side BC is twice side AB. If △ACQ ~ △BAP, find area of △BAP : area of △ACQ.
Similarity
59 Likes
Answer
Given,
ABCD is a rectangle where side BC is twice side AB.
⇒ BC = 2AB
In right angled triangle ABC,
By pythagoras theorem,
⇒ AC2 = AB2 + BC2
⇒ AC2 = AB2 + (2AB)2
⇒ AC2 = AB2 + 4AB2
⇒ AC2 = 5AB2
⇒ AC = AB.
We know that,
The ratio of the area of two similar triangles is equal to the square of the ratio of any pair of the corresponding sides of the similar triangles.
Area of △BAP : Area of △ACQ = 1 : 5.
Hence, Area of △BAP : Area of △ACQ = 1 : 5.
Answered By
22 Likes
Related Questions
Determine the ratio in which the line y = 2 + 3x divides the line segment AB joining the points A(-3, 9) and B(4, 2).
Square ABCD lies in the third quadrant of a XY plane such that its vertex A is at (-3, -1) and the diagonal DB produced is equally inclined to both the axes. The diagonals AC and BD meets at P(-2, -2). Find the :
(a) Slope of BD
(b) equation of AC
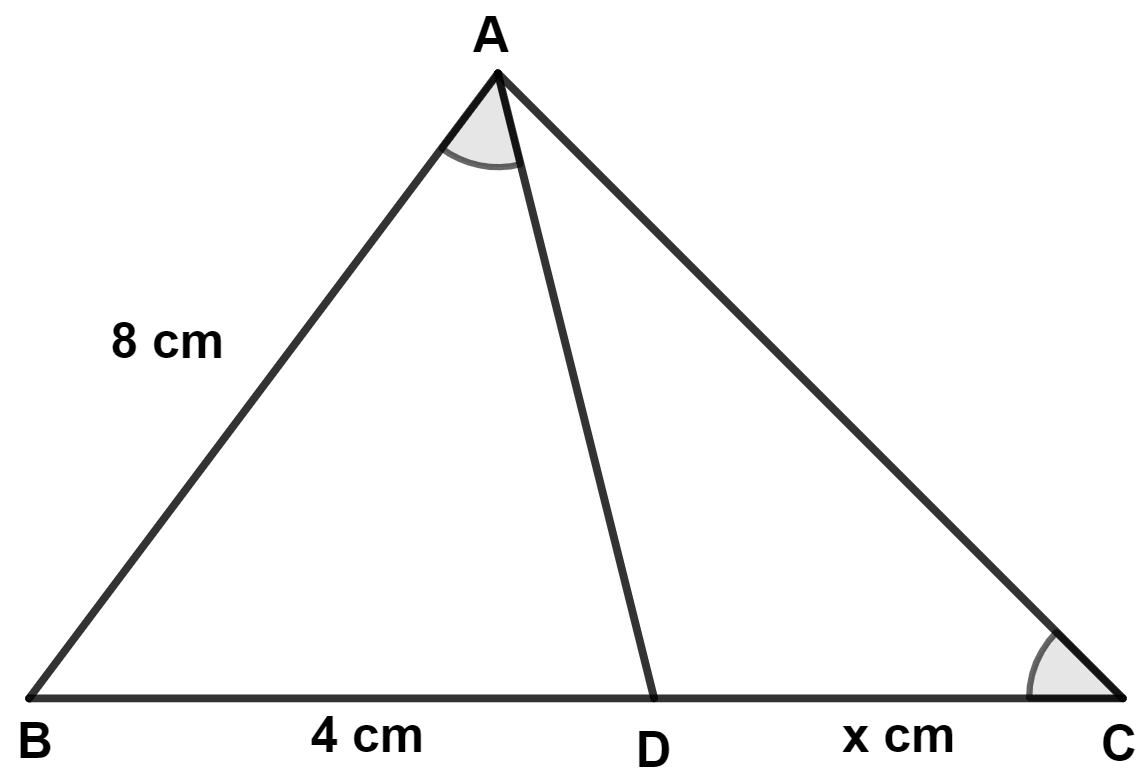
Given a triangle ABC, and D is a point on BC such that BD = 4 cm and DC = x cm. If ∠BAD = ∠C and AB = 8 cm, then,
(a) prove that triangle ABD is similar to triangle CBA.
(b) find the value of 'x'.
In the extract of Survey of India map G43S7, prepared on a scale of 2 cm to 1 km, a child finds the length of the cart track between two settlements is 7.6 cm. Find :
(a) the actual length of the cart track on the ground.
(b) actual area of a grid square, if each has an area of 4 cm2.