Mathematics
AB is a line segment and M is its mid-point. Three semi-circles are drawn with AM, MB and AB as diameters on the same side of the line AB. A circle with radius r unit is drawn so that it touches all the three semi-circles. Show that : AB = 6 × r.
Circles
2 Likes
Answer
From figure,
OR = OS = r.

AP = PM = MQ = QB =
Also,
As, RP = SQ = PM [Radius of semi-circle with center P]
⇒ OP = OR + RP = r + ,
⇒ OQ = OS + SQ = r + ,
⇒ OM = LM - OL =
In right angle △OPM,
OP2 = OM2 + PM2
Hence, proved that AB = 6 × r.
Answered By
3 Likes
Related Questions
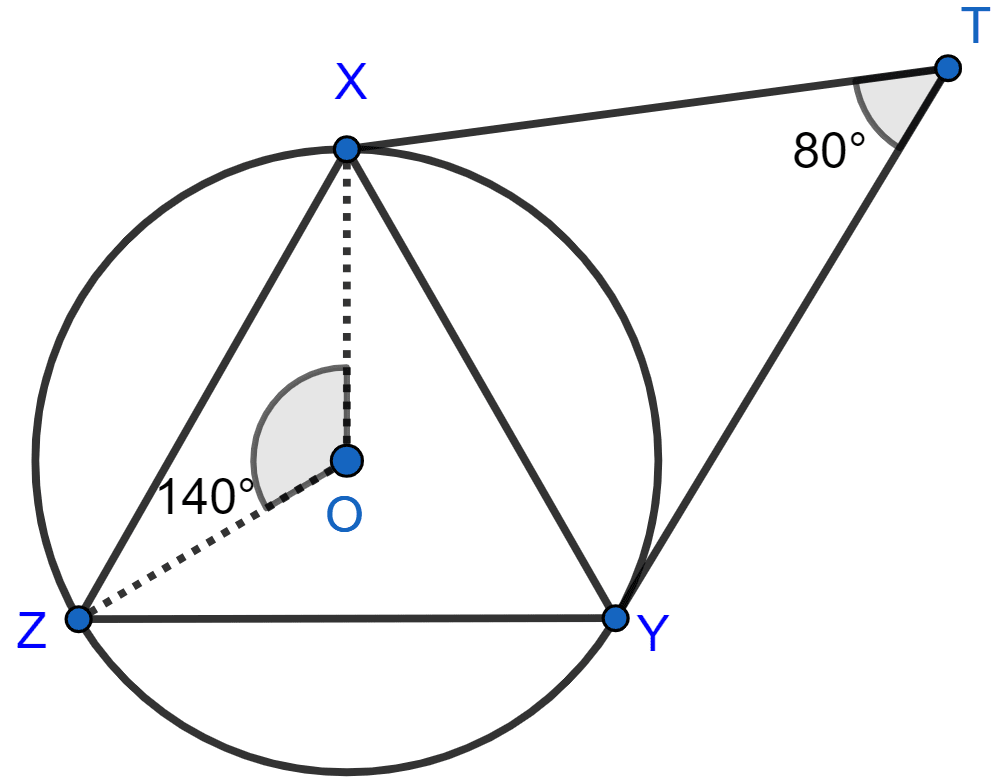
In the figure, given below, O is the center of the circumcircle of triangle XYZ. Tangents at X and Y intersect at point T. Given ∠XTY = 80° and ∠XOZ = 140°, calculate the value of ∠ZXY.
In the given figure, AE and BC intersect each other at point D. If ∠CDE = 90°, AB = 5 cm, BD = 4 cm and CD = 9 cm, find AE.

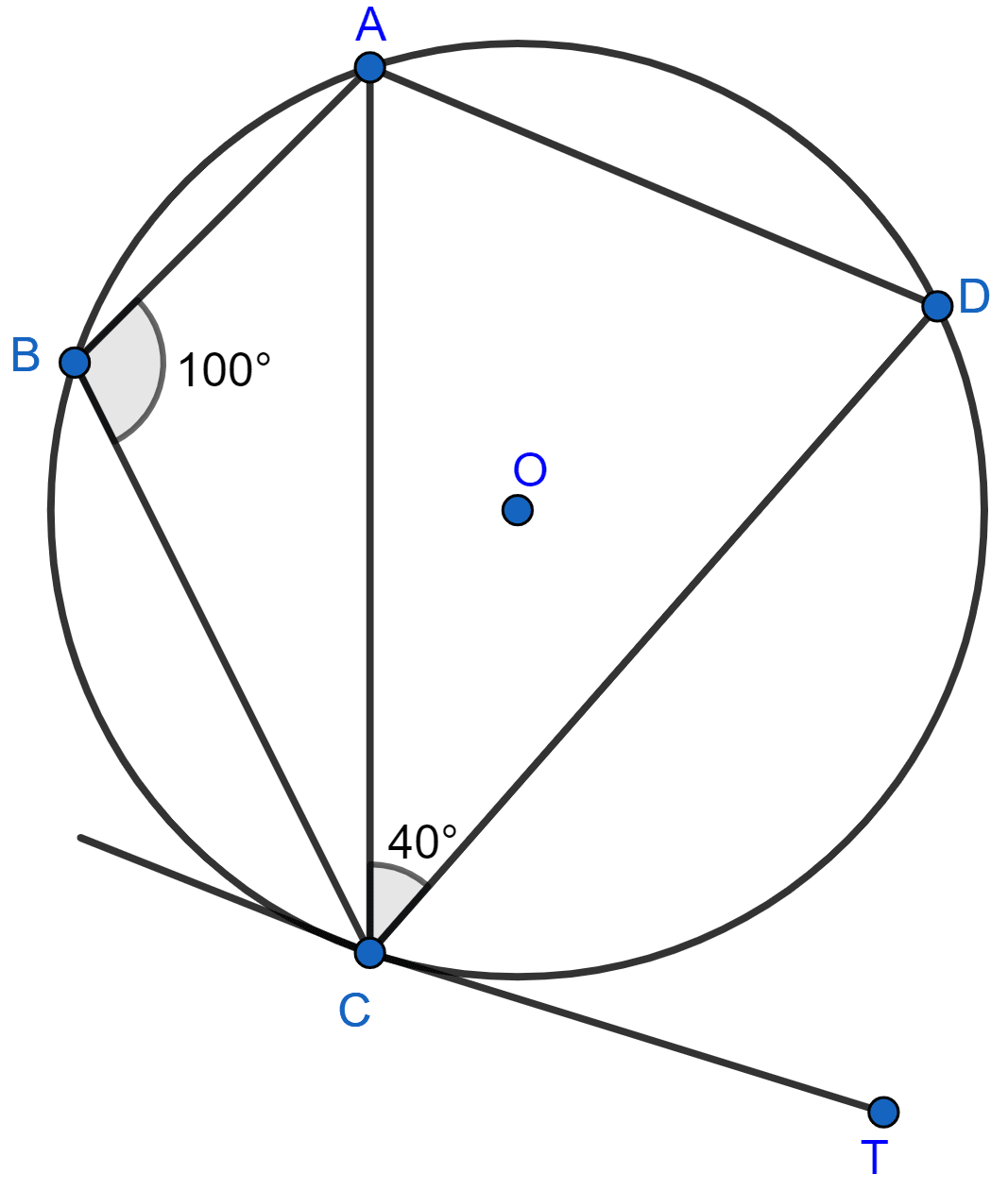
In the given circle with centre O, angle ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.
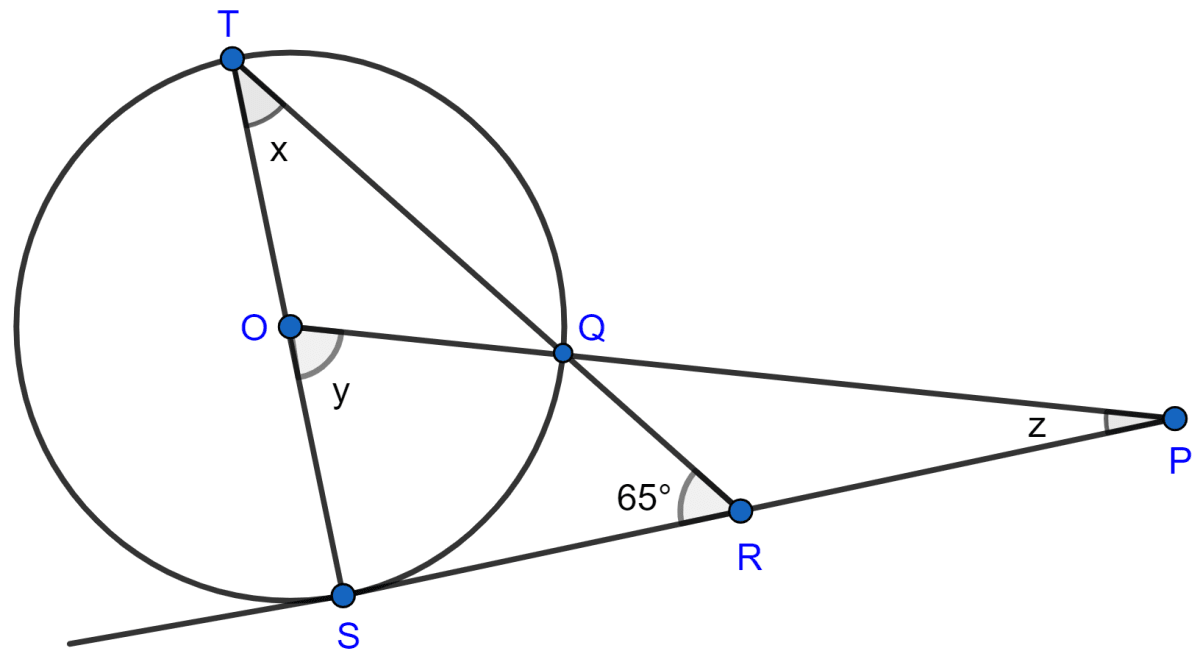
In the figure given below, O is the center of the circle and SP is a tangent. If ∠SRT = 65°, find the values of x, y and z.