Mathematics
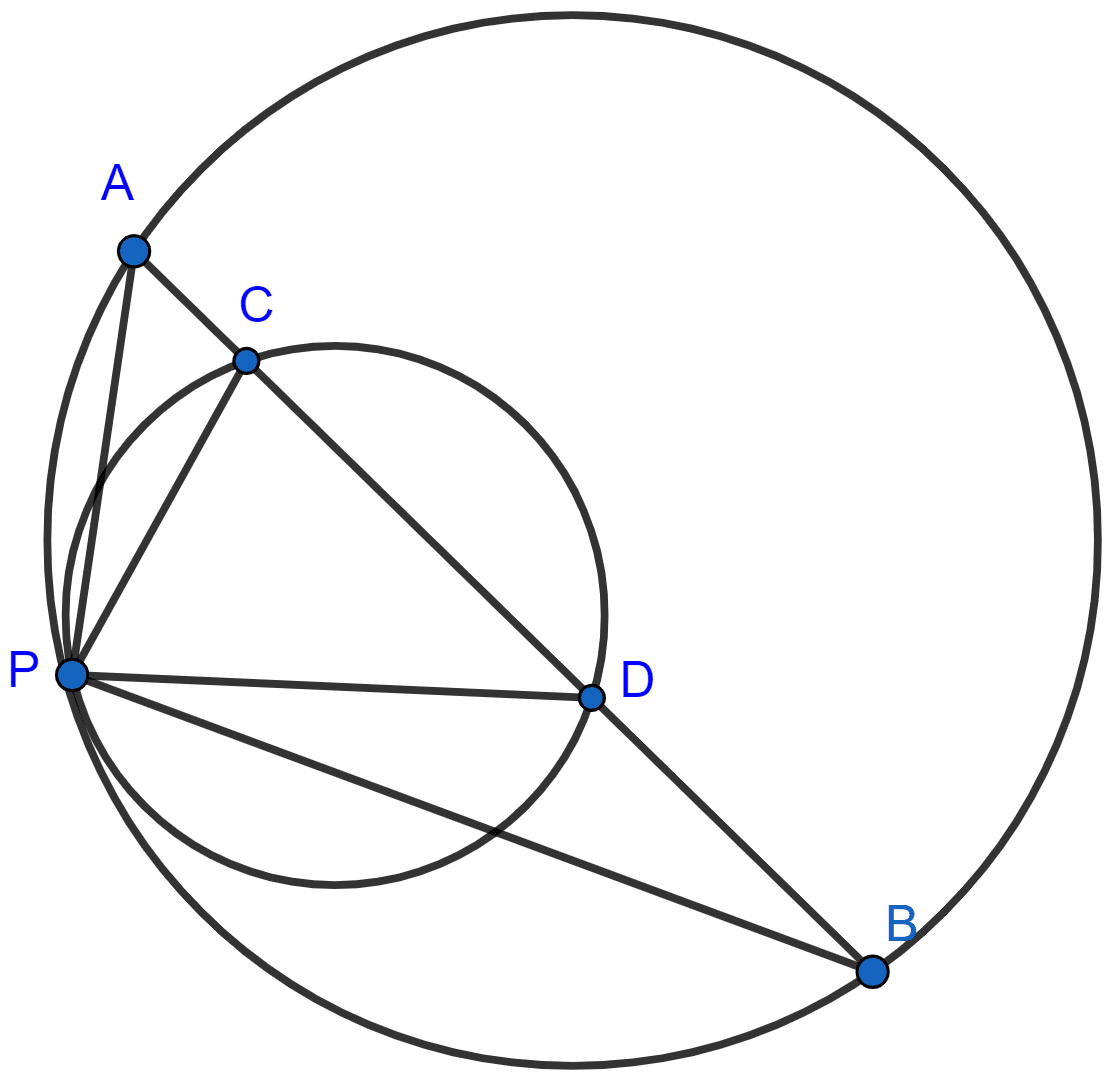
AB and CD are two chords of a circle intersecting at point P inside the circle. If
(i) AB = 24 cm, AP = 4 cm and PD = 8 cm, determine CP.
(ii) AP = 3 cm, PB = 2.5 cm and CD = 6.5 cm, determine CP.
Circles
8 Likes
Answer
(i) From figure,
⇒ AB = AP + PB
⇒ 24 = 4 + PB
⇒ PB = 24 - 4
⇒ PB = 20 cm.
We know that,
If two chords intersect in a circle, then the products of the measures of the segments of the chords are equal.
⇒ AP × PB = CP × PD
⇒ 4 × 20 = CP × 8
⇒ 80 = 8CP
⇒ CP = = 10.
Hence, CP = 10 cm.
(ii) Let CP = x, so PD = (6.5 - x).
We know that,
If two chords intersect in a circle , then the products of the measures of the segments of the chords are equal.
⇒ AP × PB = CP × PD
⇒ 3 × 2.5 = x(6.5 - x)
⇒ 7.5 = 6.5x - x2
⇒ x2 - 6.5x + 7.5 = 0
⇒ x2 - 5x - 1.5x + 7.5 = 0
⇒ x(x - 5) - 1.5(x - 5) = 0
⇒ (x - 1.5)(x - 5) = 0
⇒ x - 1.5 = 0 or x - 5 = 0
⇒ x = 1.5 or x = 5.
Hence, CP = 1.5 cm or 5 cm.
Answered By
2 Likes
Related Questions
In the given figure, ∠ABC = 90° and BC is diameter of the given circle. Show that :
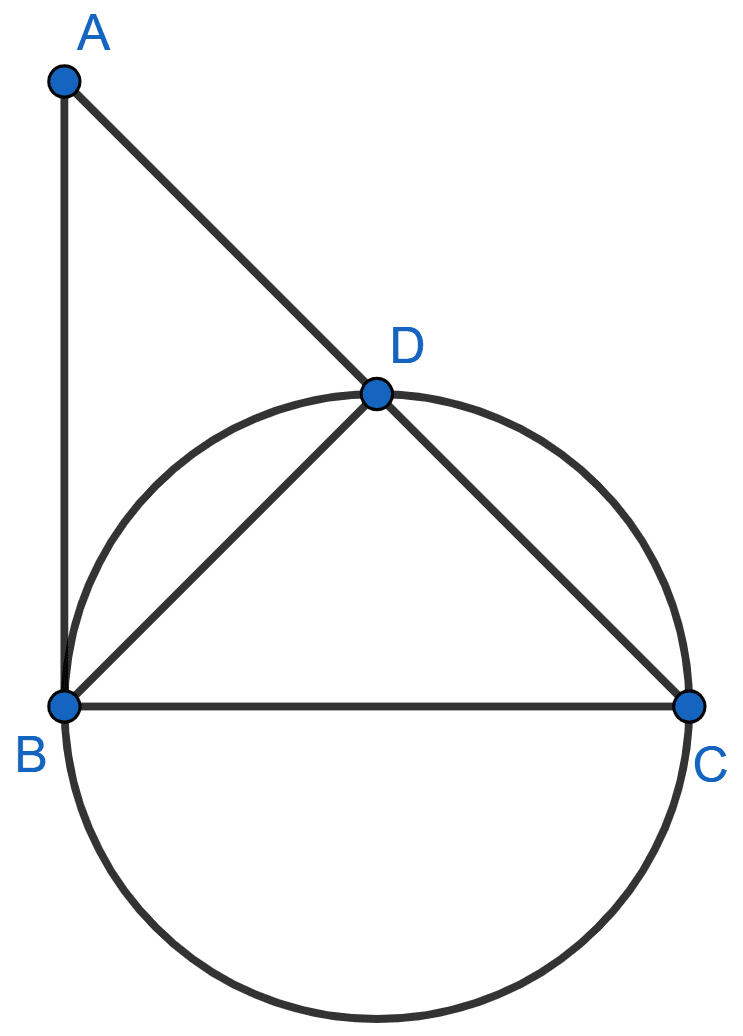
(i) AC × AD = AB2
(ii) AC × CD = BC2
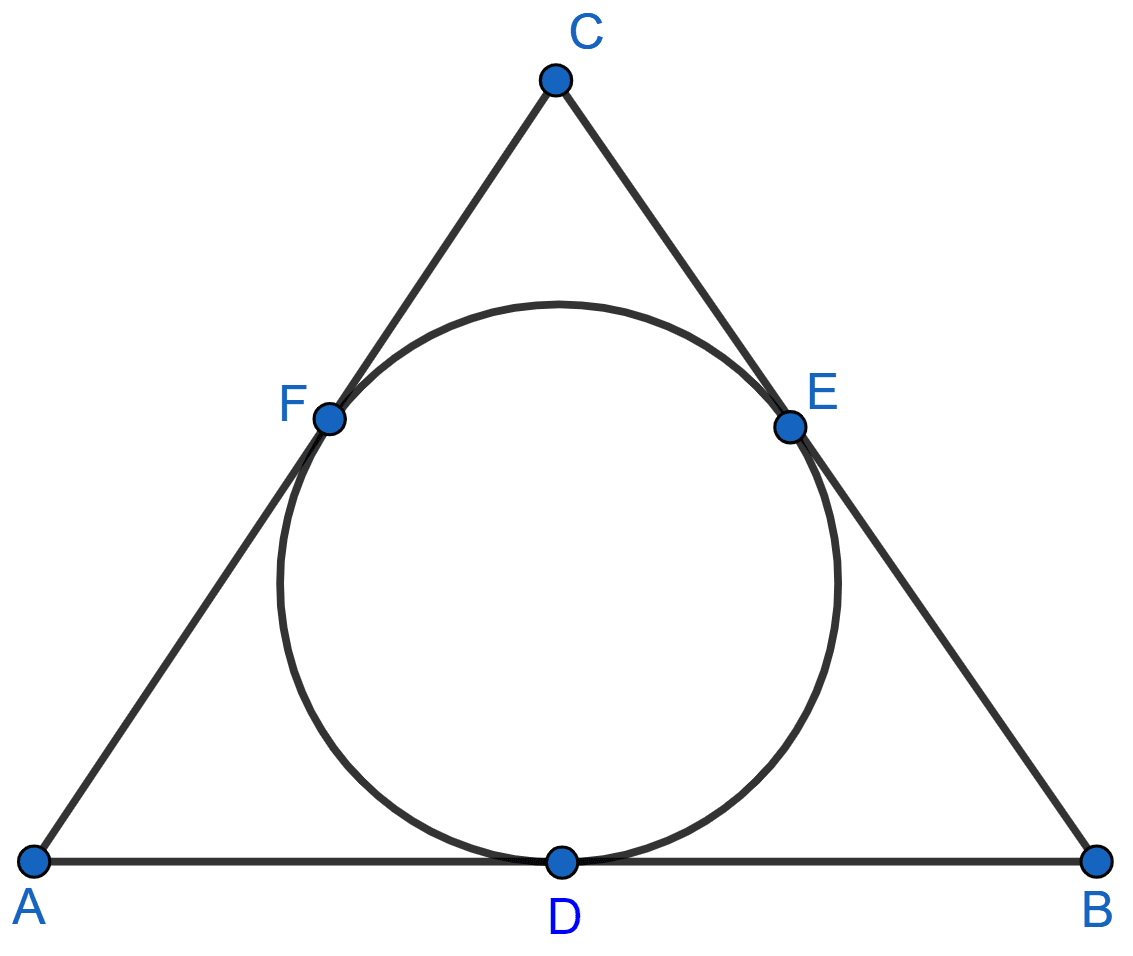
In the given figure, AB, BC and CA are tangents to the given circle. If AB = 12 cm, BC = 8 cm and AC = 10 cm, find the lengths of AD, BE and CF.
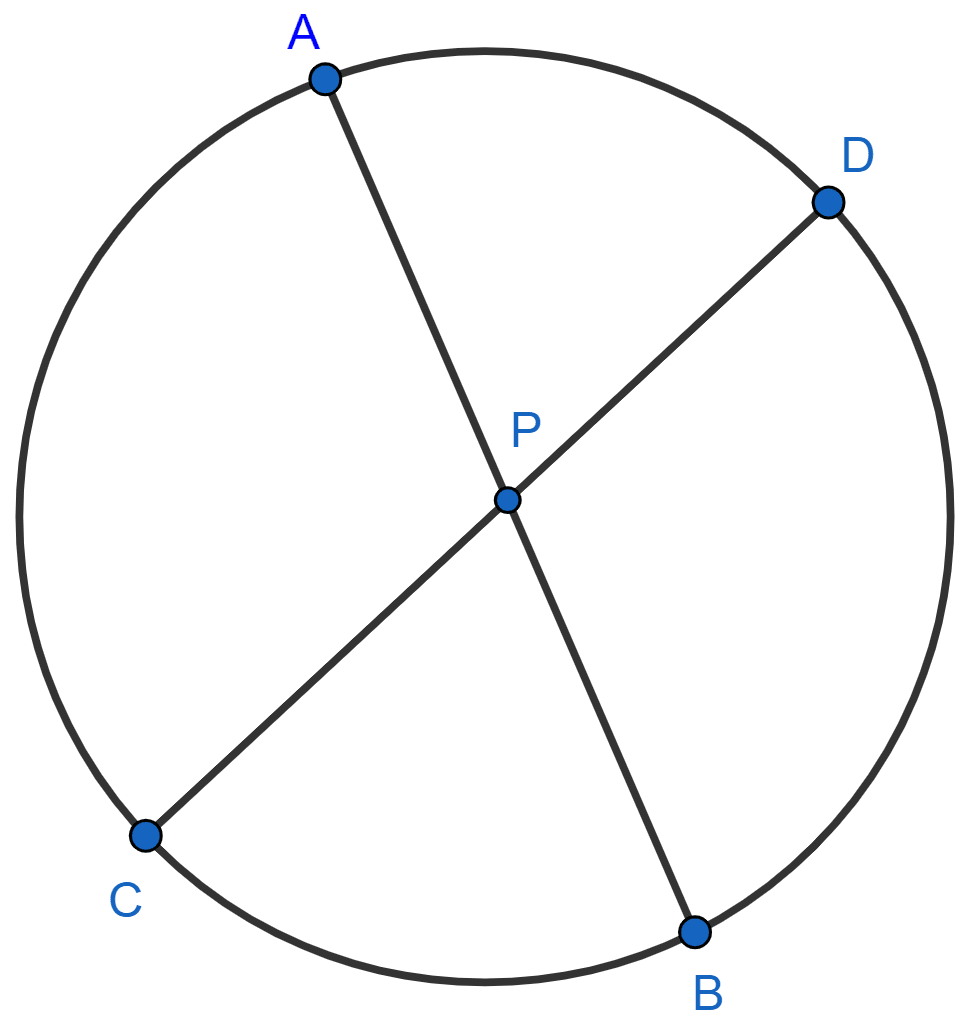
AB and CD are two chords of a circle intersecting at point P outside the circle. If
(i) PA = 8 cm, PC = 5 cm and PD = 4 cm, determine AB.
(ii) PC = 30 cm, CD = 14 cm and PA = 24 cm, determine AB.
Two circles touch each other internally at a point P. A chord AB of the bigger circle intersects the other circle in C and D. Prove that : ∠CPA = ∠DPB.