Mathematics
In the given figure, ∠ABC = 90° and BC is diameter of the given circle. Show that :
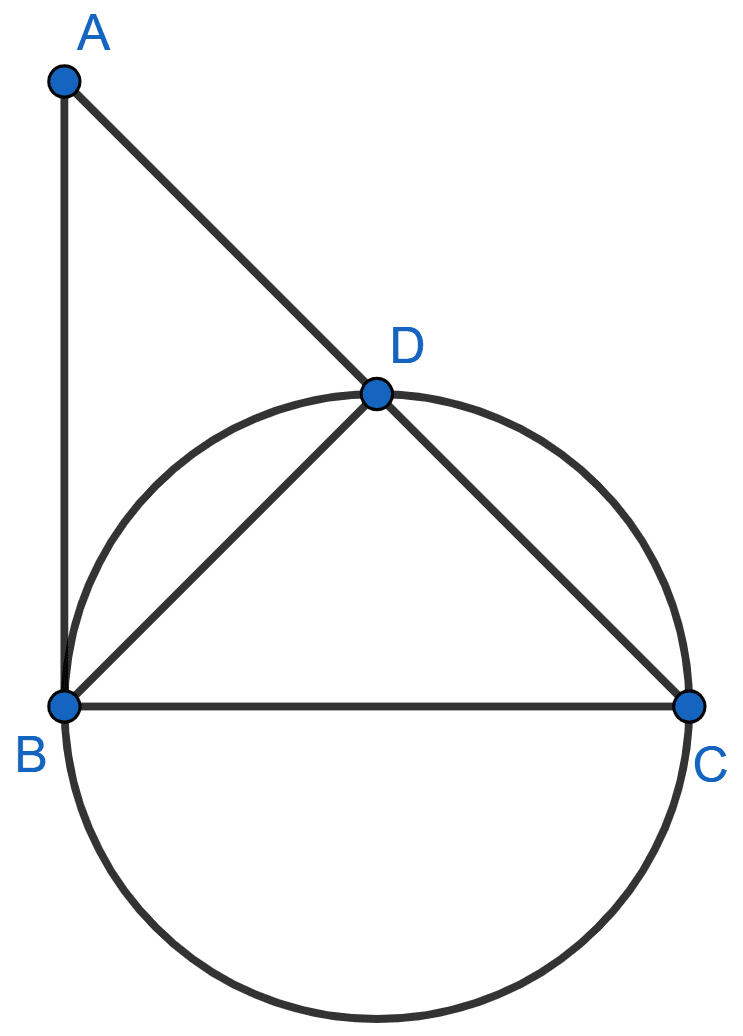
(i) AC × AD = AB2
(ii) AC × CD = BC2
Circles
6 Likes
Answer
(i) As, BC is the diameter.
We know that,
Angle in a semicircle is a right angle.
∴ ∠BDC = 90°
From figure,
⇒ ∠BDC + ∠BDA = 180° [Linear Pair]
⇒ 90° + ∠BDA = 180°
⇒ ∠BDA = 180° - 90°
⇒ ∠BDA = 90°.
As, AB is the tangent and BC is diameter and tangent at any point and line from that point to center are perpendicular to each other.
⇒ ∠ABC = 90°
In △ABC and △ABD,
∠ABC = ∠ADB (Both equal to 90°)
∠BAD = ∠BAC (Common)
∴ △ABC ~ △ABD
In similar triangles,
Ratio of corresponding sides are in equal proportion.
Hence, proved that AB2 = AC × AD.
(ii) In △ABC and △BDC,
⇒ ∠ABC = ∠BDC (Both equal to 90°)
⇒ ∠BCA = ∠BCD (Common)
∴ △ABC ~ △BDC
In similar triangles,
Ratio of corresponding sides are in equal proportion.
Hence, proved that BC2 = AD × CD.
Answered By
1 Like
Related Questions
In the given figure, AC = AB and ∠ABC = 72°. OA and OB are two tangents. Determine :
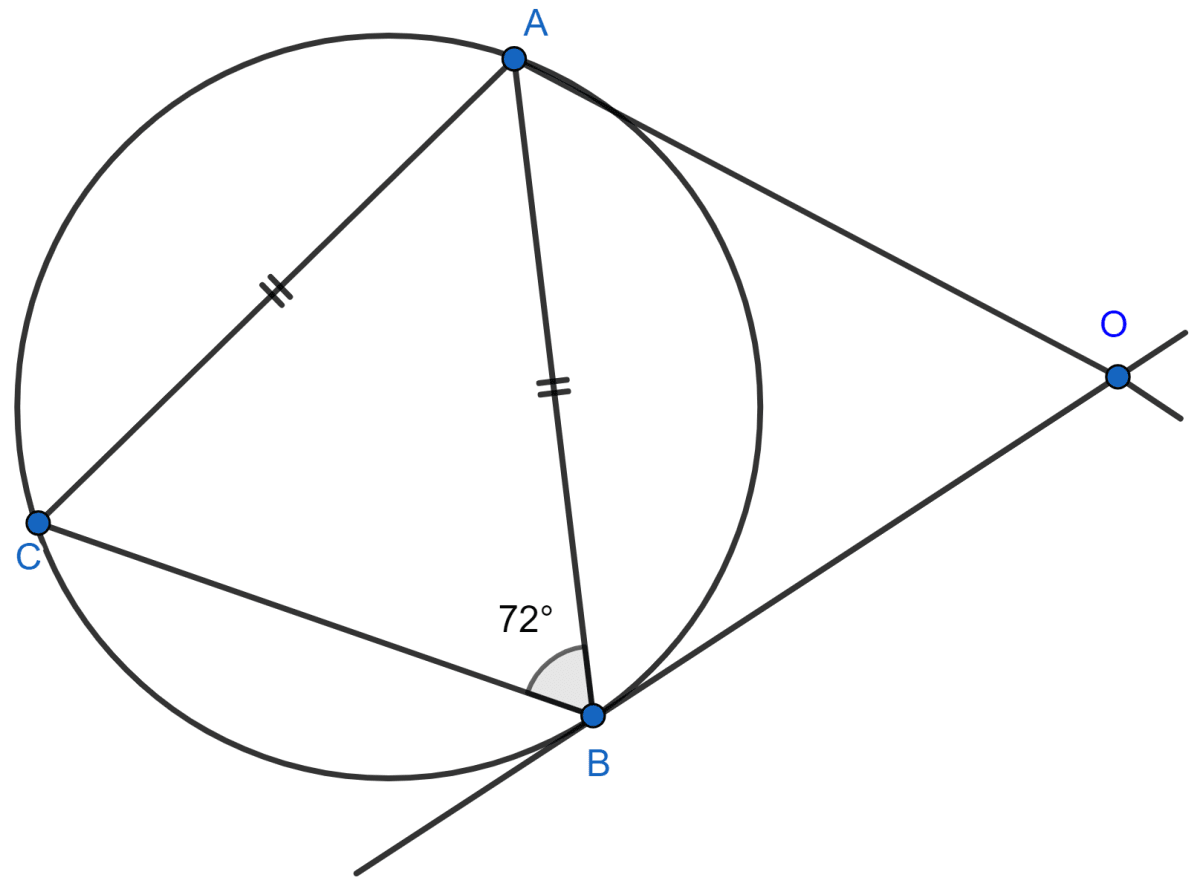
(i) ∠AOB
(ii) angle subtended by the chord AB at the center.
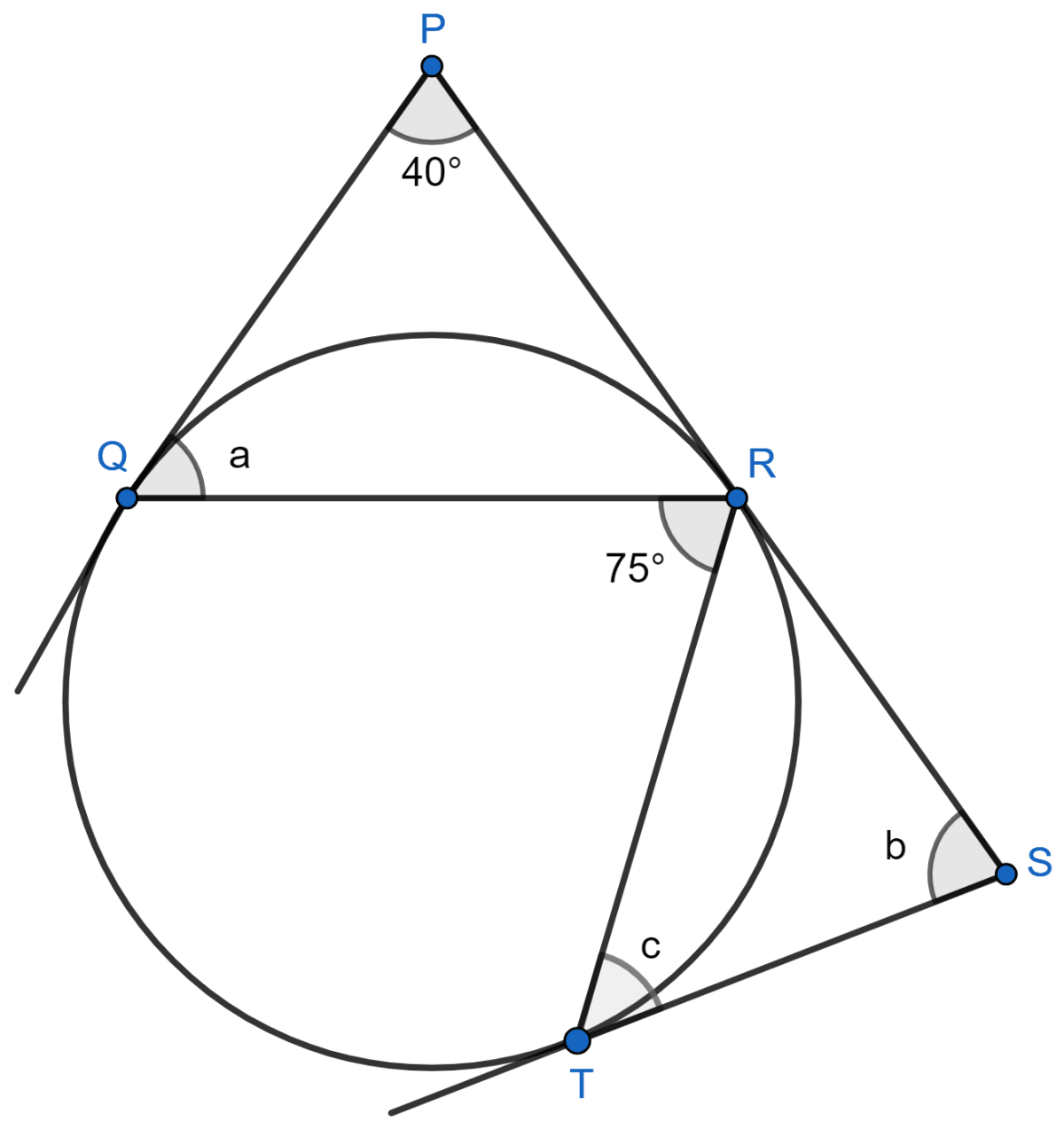
In the given figure, PQ, PR and ST are tangents to the same circle. If ∠P = 40° and ∠QRT = 75°, find a, b and c.
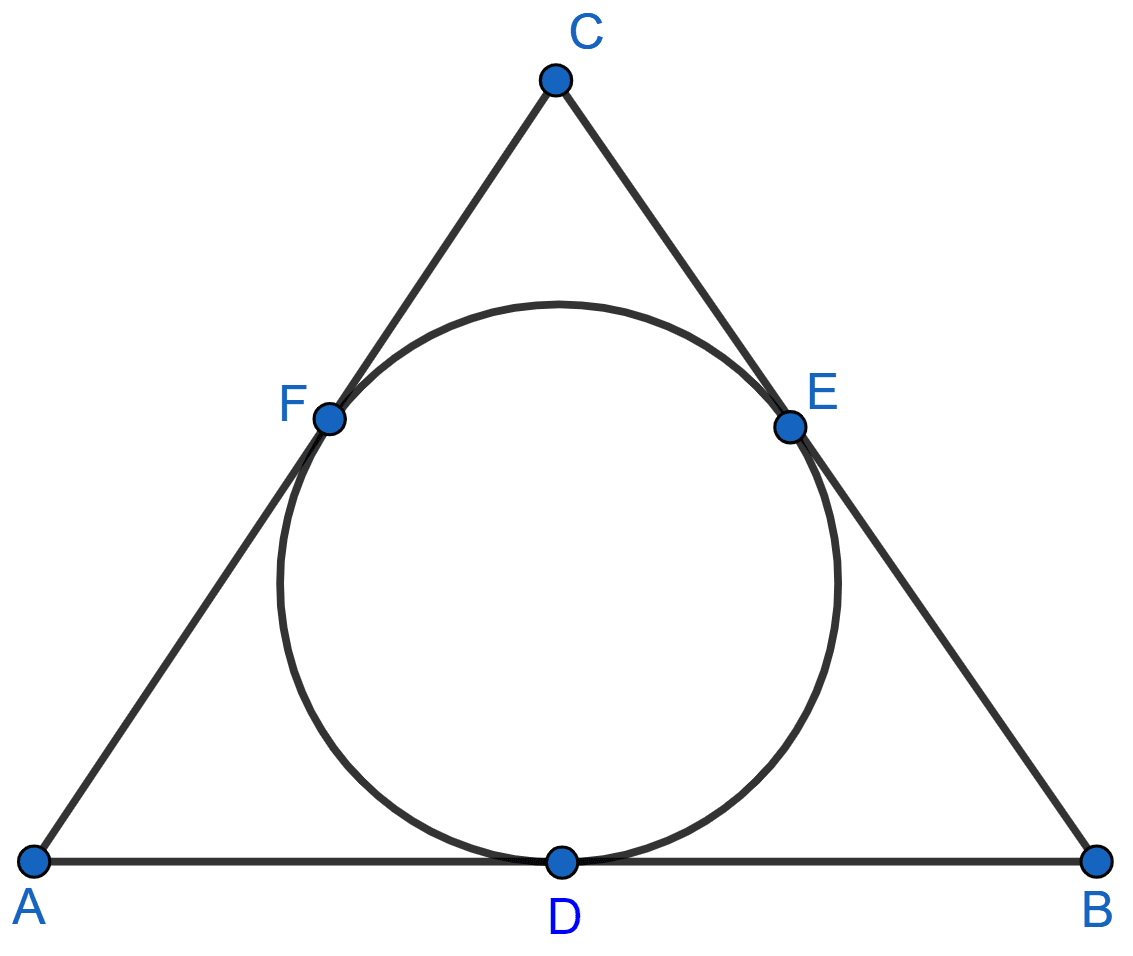
In the given figure, AB, BC and CA are tangents to the given circle. If AB = 12 cm, BC = 8 cm and AC = 10 cm, find the lengths of AD, BE and CF.
AB and CD are two chords of a circle intersecting at point P inside the circle. If
(i) AB = 24 cm, AP = 4 cm and PD = 8 cm, determine CP.
(ii) AP = 3 cm, PB = 2.5 cm and CD = 6.5 cm, determine CP.