Mathematics
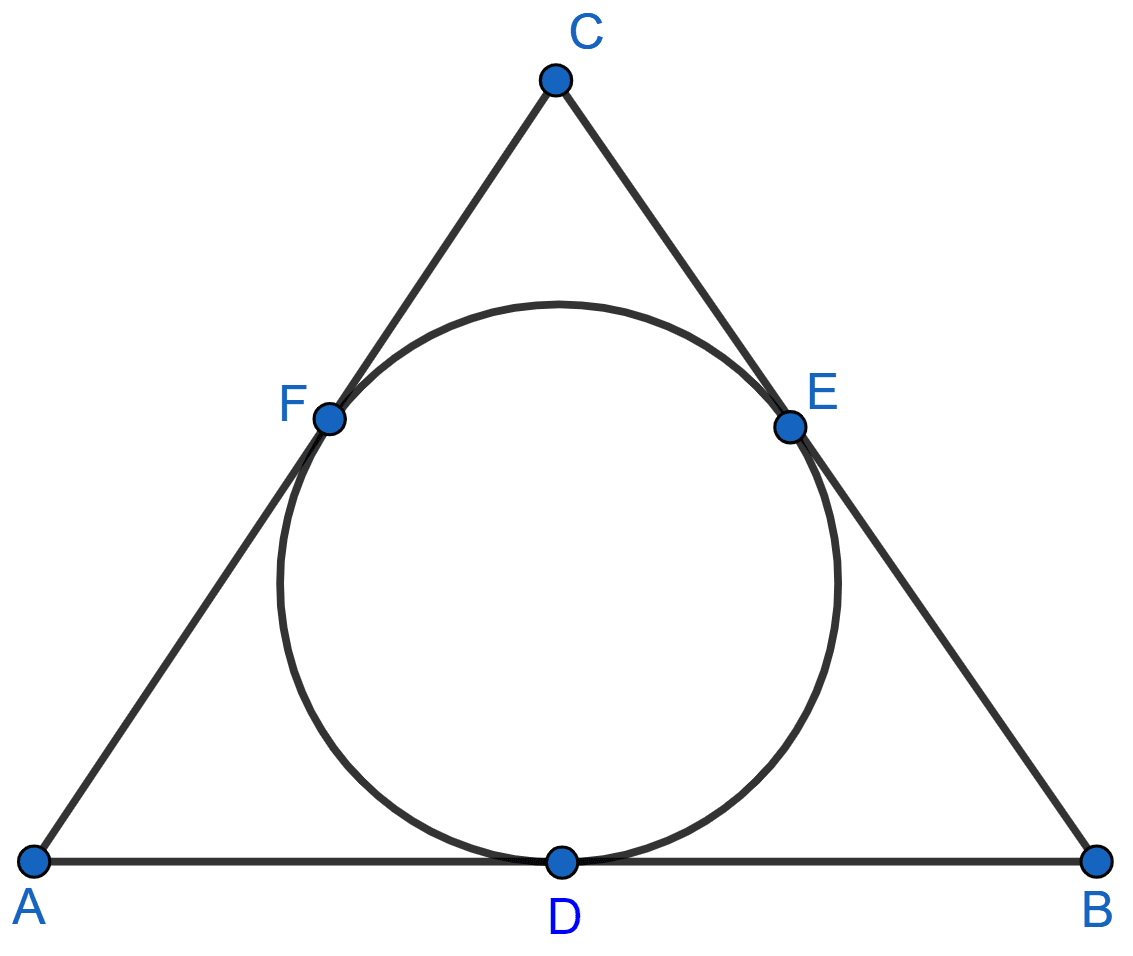
In the given figure, AB, BC and CA are tangents to the given circle. If AB = 12 cm, BC = 8 cm and AC = 10 cm, find the lengths of AD, BE and CF.
Circles
3 Likes
Answer
As, tangents from an exterior fixed point to a circle are equal in length,
Let,
AD = AF = x cm
BD = BE = y cm
CF = CE = z cm
From figure,
⇒ AD + BD = AB
⇒ x + y = 12 ………(1)
⇒ AF + CF = AC
⇒ x + z = 10 ……..(2)
⇒ BE + CE = BC
⇒ y + z = 8 ……….(3)
Subtracting eq (3) from (1), we get :
⇒ x + y - (y + z) = 12 - 8
⇒ x - z = 4 …………(4)
Adding equation (2) and (4), we get :
⇒ (x + z) + (x - z) = 10 + 4
⇒ 2x = 14
⇒ x =
⇒ x = 7.
Substituting value of x in equation (1), we get :
⇒ 7 + y = 12
⇒ y = 12 - 7
⇒ y = 5.
Substituting value of y in equation (3), we get :
⇒ y + z = 8
⇒ 5 + z = 8
⇒ z = 8 - 5
⇒ z = 3.
∴ AD = x = 7, BE = y = 5 and CF = z = 3.
Hence, AD = 7 cm, BE = 5 cm and CF = 3 cm.
Answered By
2 Likes
Related Questions
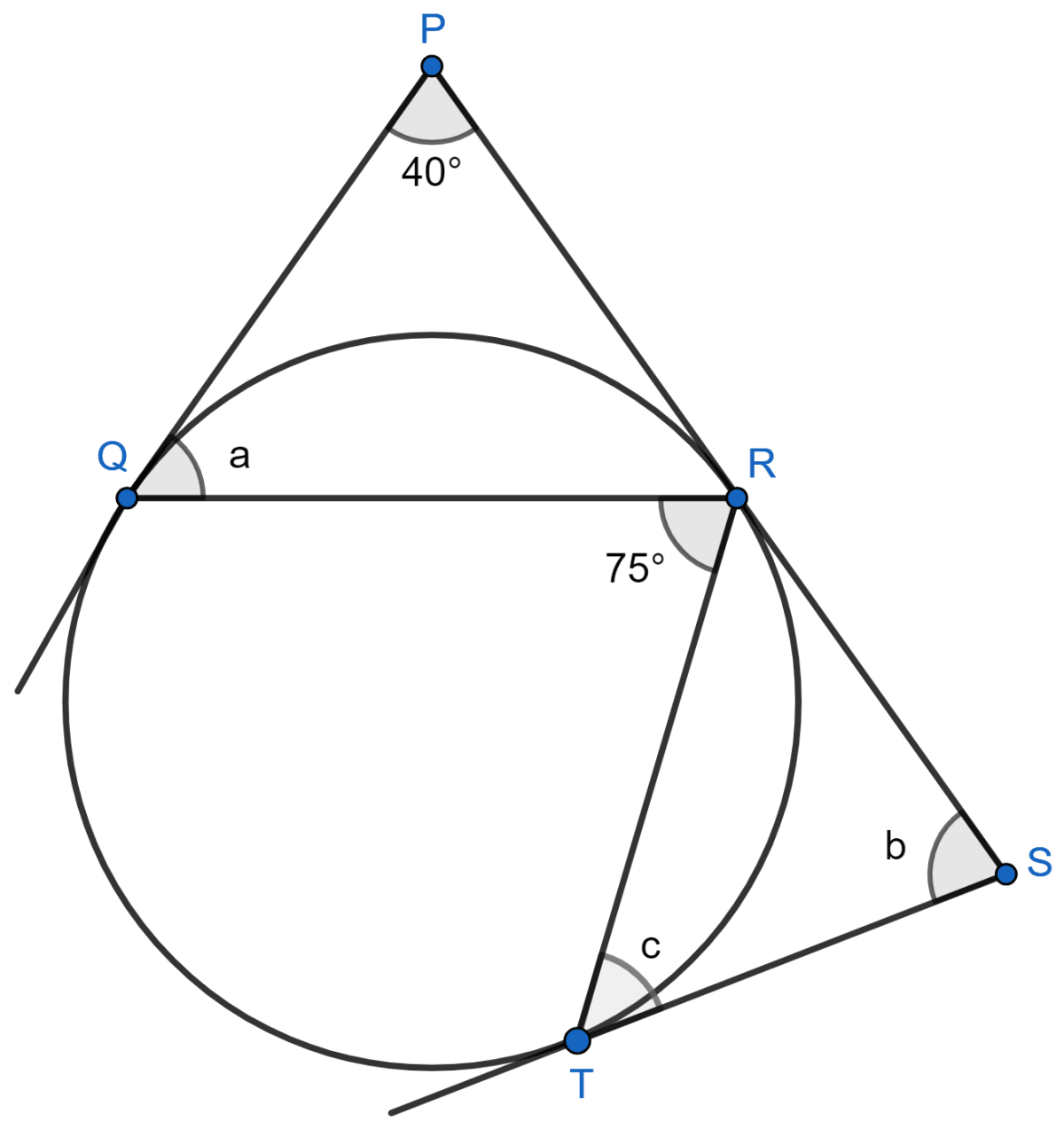
In the given figure, PQ, PR and ST are tangents to the same circle. If ∠P = 40° and ∠QRT = 75°, find a, b and c.
In the given figure, ∠ABC = 90° and BC is diameter of the given circle. Show that :
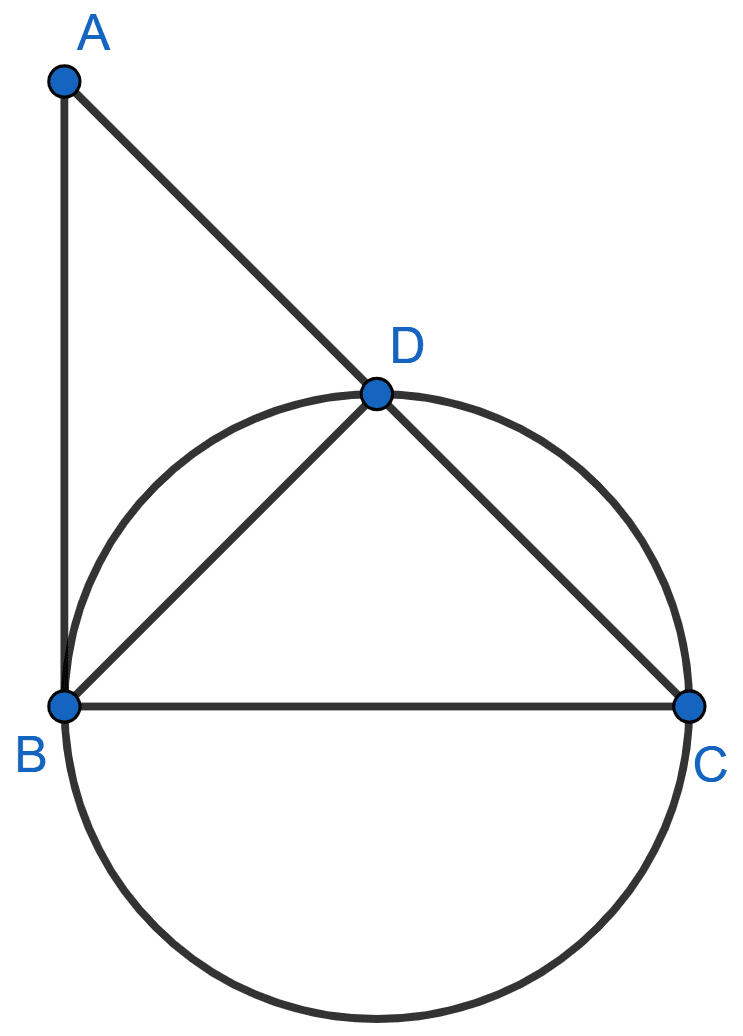
(i) AC × AD = AB2
(ii) AC × CD = BC2
AB and CD are two chords of a circle intersecting at point P inside the circle. If
(i) AB = 24 cm, AP = 4 cm and PD = 8 cm, determine CP.
(ii) AP = 3 cm, PB = 2.5 cm and CD = 6.5 cm, determine CP.
AB and CD are two chords of a circle intersecting at point P outside the circle. If
(i) PA = 8 cm, PC = 5 cm and PD = 4 cm, determine AB.
(ii) PC = 30 cm, CD = 14 cm and PA = 24 cm, determine AB.