A(2, 5), B(-1, 2) and C(5, 8) are the vertices of a triangle ABC, 'M' is a point on AB such that AM : MB = 1 : 2. Find the coordinates of 'M'. Hence, find the equation of the line passing through C and M.

The triangle ABC is shown in the figure below:

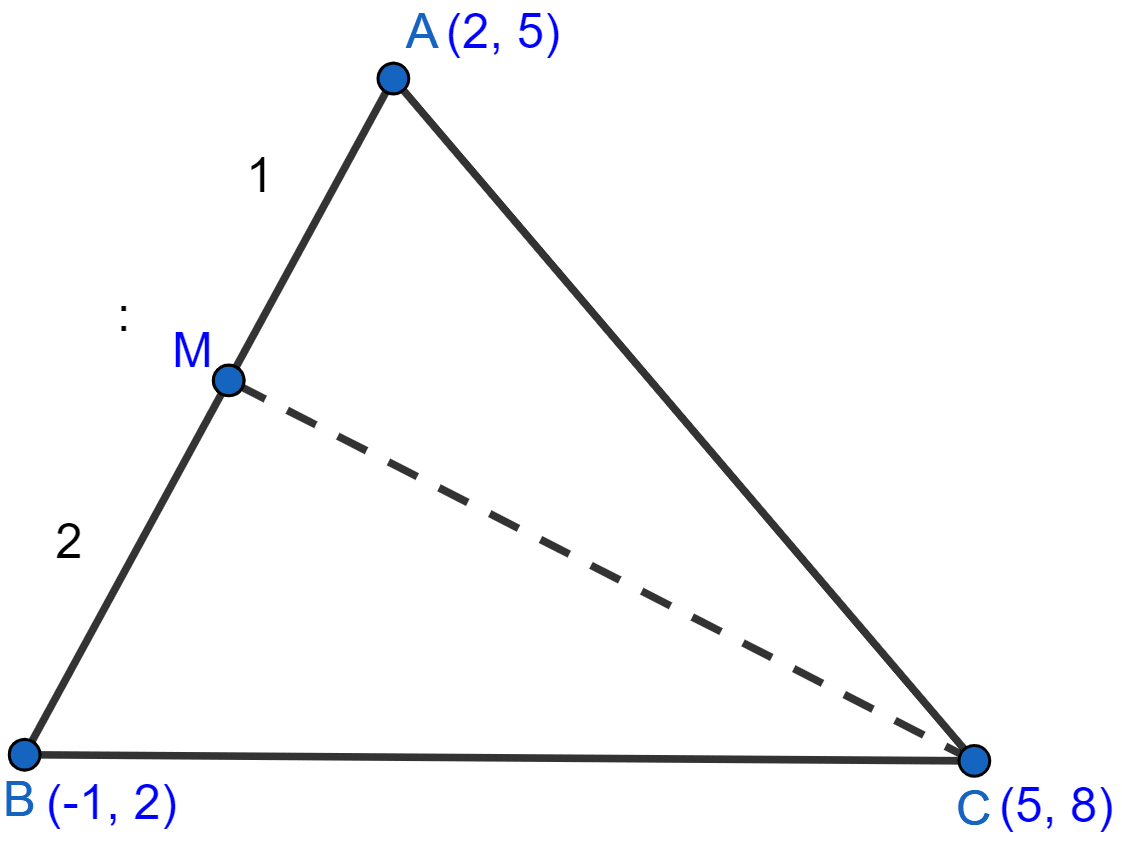
Given AM : MB = 1 : 2. By section-formula the coordinates of M are,

$\Big(\dfrac{m$1x2 + m2x1}{m1 + m2}, \dfrac{m1y2 + m2y1}{m1 + m2}\Big)

Putting values we get,

$= \Big(\dfrac{1 \times -1 + 2 \times 2}{1 + 2}, \dfrac{1 \times 2 + 2 \times 5}{1 + 2}\Big) \\[1em] = \Big(\dfrac{-1 + 4}{3}, \dfrac{2 + 10}{3}) \\[1em] = \Big(\dfrac{3}{3}, \dfrac{12}{3}\Big) \\[1em] = (1, 4).$

Equation of line CM can be given by two-point formula i.e.,

$y - y$1 = \dfrac{y2 - y1}{x2 - x1}(x - x1)

Putting values in above equation we get,

$\Rightarrow y - 8 = \dfrac{4 - 8}{1 - 5}(x - 5) \\[1em] \Rightarrow y - 8 = \dfrac{-4}{-4}(x - 5) \\[1em] \Rightarrow y - 8 = 1 \times (x - 5) \\[1em] \Rightarrow y - 8 = x - 5 \\[1em] \Rightarrow x - y - 5 + 8 = 0 \\[1em] \Rightarrow x - y + 3 = 0.$

Hence, the equation of CM is x - y + 3 = 0 and the coordinates of M are (1, 4).