Mathematics
A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
Triangles
Answer
Let AB be the pole of length 6 m and BC = 4 m is the shadow of pole AB.
Let PQ be the tower and QR = 28 m is the shadow of the tower PQ.
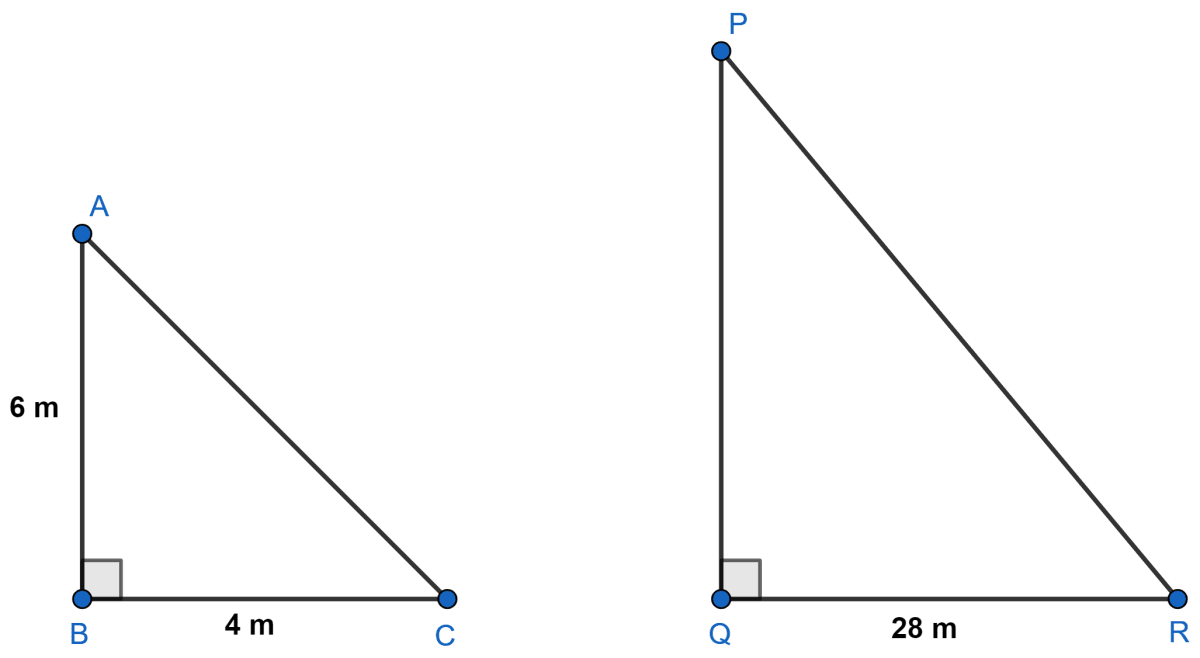
In Δ ABC and Δ PQR,
⇒ ∠ABC = ∠PQR (Both equal to 90°.)
⇒ ∠BAC = ∠QPR (Sunray falls on the pole and tower at the same angle, at the same time)
⇒ Δ ABC ∼ Δ PQR (By A.A. axiom)
We know that,
If two triangles are similar then their corresponding sides are proportional.
Hence, the height of the tower is 42 m.
Answered By
Related Questions
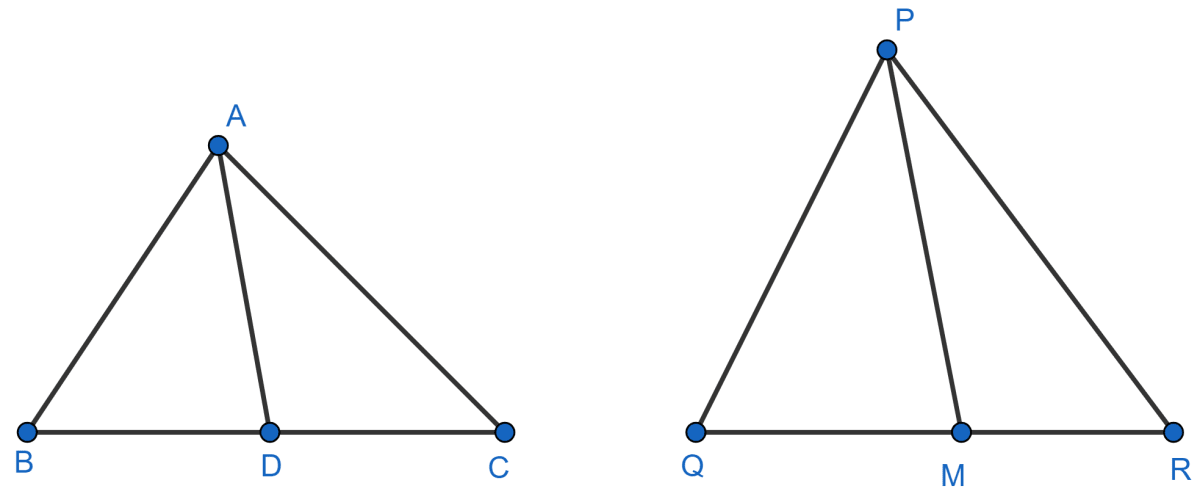
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of △ PQR. Show that △ ABC ~ △ PQR.
D is a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC. Show that CA2 = CB.CD.
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that Δ ABC ~ Δ PQR.
If AD and PM are medians of triangles ABC and PQR, respectively where Δ ABC ~ Δ PQR, prove that .