Mathematics
A pole of height 5 m is fixed on the top of a tower. The angle of elevation of the top of pole as observed from a point A on the ground is 60° and the angle of depression of the point A from the top of the tower is 45°. Find the height of the tower. (Take )
Heights & Distances
71 Likes
Answer
Let the height of tower (BC) be h meters and BD be the pole of height 5 meters above it.
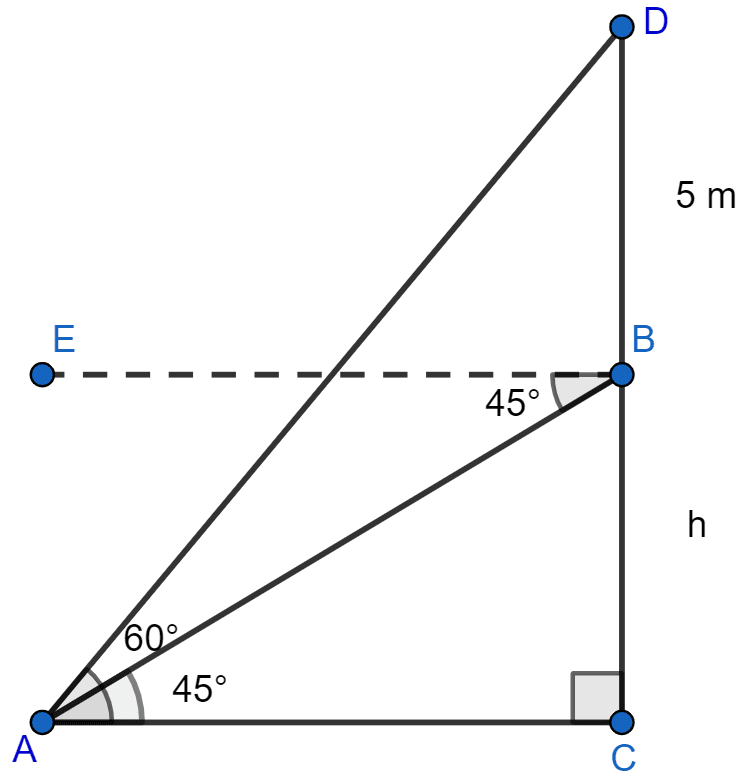
From figure,
∠BAC = ∠EBA = 45° (Alternate angles are equal)
DC = DB + BC = 5 + h.
Considering right angled △BCA, we get
Considering right angled △DCA, we get
Putting value of AC from Eq 1 in above equation we get,
Hence, the height of the tower is 6.83 meters.
Answered By
22 Likes
Related Questions
A man 1.8 m high stands at a distance of 3.6 m from a lamp post and casts a shadow of 5.4 m on the ground. Find the height of the lamp post.
The angles of depression of the top and the bottom of a 8 m tall building from the top of a multi-storeyed building are 30° and 45° respectively. Find the height of the multi storeyed building and the distance between the two buildings, correct to two decimal places.
A vertical pole and a vertical tower are on the same level ground. From the top of the pole, the angle of elevation of the top of the tower is 60° and the angle of depression of the foot of tower is 30°. Find the height of the tower if the height of the pole is 20 m.
From the top of a building 20 m high, the angle of elevation of the top of a monument is 45° and the angle of depression of its foot is 15°. Find the height of the monument.