KnowledgeBoat Logo

Mathematics

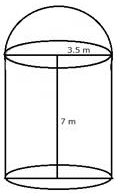
A metal container in the form of a cylinder is surmounted by a hemisphere of the same radius. The internal height of the cylinder is 7 m and the internal radius is 3.5 m. Calculate :

(i) the total area of the internal surface, excluding the base;

(ii) the internal volume of the container in m3.

Mensuration

8 Likes

Answer

Given,

Radius of cylindrical portion = Radius of hemispherical portion = r = 3.5 m.

Height of cylinder (h) = 7 m.

A metal container in the form of a cylinder is surmounted by a hemisphere of the same radius. The internal height of the cylinder is 7 m and the internal radius is 3.5 m. Calculate : (i) the total area of the internal surface, excluding the base; (ii) the internal volume of the container in m<sup>3</sup>. Cylinder, Cone, Sphere, Concise Mathematics Solutions ICSE Class 10.

(i) Area of internal surface = Surface area of cylinder + Surface area of hemisphere

= 2πrh + 2πr2

= 2πr(h + r)

= 2×227×3.5×(7+3.5)2 \times \dfrac{22}{7} \times 3.5 \times (7 + 3.5)

= 2 × 22 × 0.5 × 10.5

= 231 m2.

Hence, the total area of the internal surface = 231 m2.

(ii) Internal volume of container = Volume of hemisphere + Volume of cylinder

=23πr3+πr2h=πr2(2r3+h)=227×(3.5)2×(2×3.53+7)=22×0.5×3.5×(73+7)=38.5×283=359.33 m3.= \dfrac{2}{3}πr^3 + πr^2h \\[1em] = πr^2\Big(\dfrac{2r}{3} + h\Big) \\[1em] = \dfrac{22}{7} \times (3.5)^2 \times \Big(\dfrac{2 \times 3.5}{3} + 7\Big) \\[1em] = 22 \times 0.5 \times 3.5 \times \Big(\dfrac{7}{3} + 7\Big) \\[1em] = 38.5 \times \dfrac{28}{3} \\[1em] = 359.33 \text{ m}^3.

Hence, volume of container = 359.33 m3.

Answered By

4 Likes

Related Questions