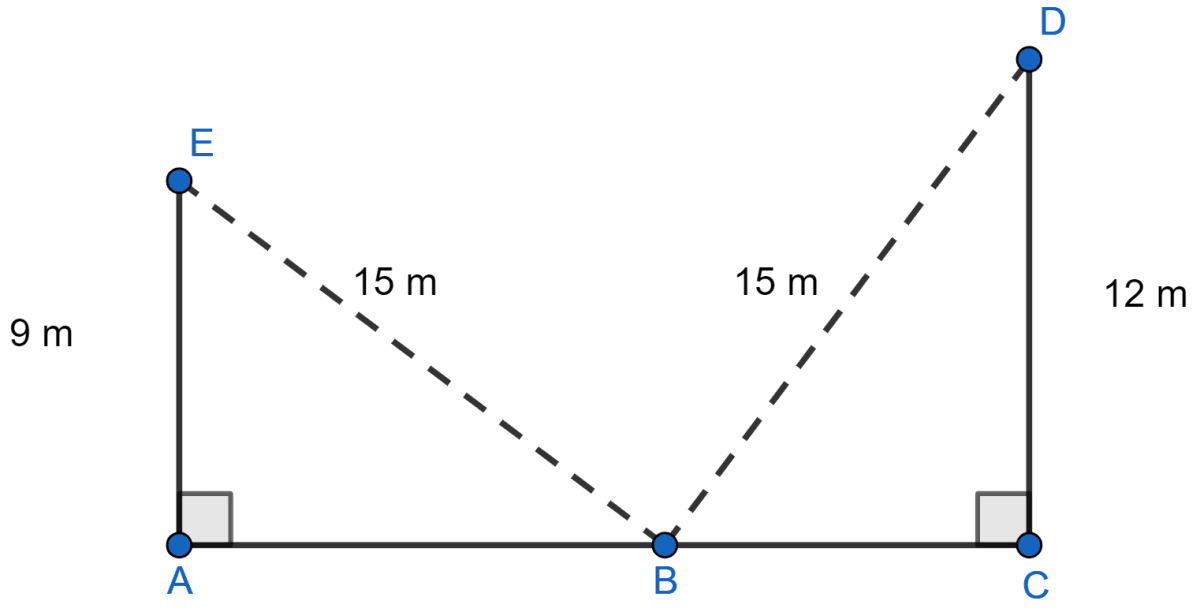
A ladder reaches a window 12 m above the ground on one side of the street. Keeping its foot at the same point, the ladder is turned to the other side of the street to reach a window 9 m high. If the length of the ladder is 15 m, then the width of the street is

1. 30 m

2. 24 m

3. 21 m

4. 18 m

In right triangle AEB,

By pythagoras theorem we get,

⇒ EB² = EA² + AB²

⇒ 15² = 9² + AB²

⇒ 225 = 81 + AB²

⇒ AB² = 144

⇒ AB = $\sqrt{144}$ = 12 m

In right triangle BCD,

By pythagoras theorem we get,

⇒ BD² = BC² + CD²

⇒ 15² = BC² + 12²

⇒ 225 = BC² + 144

⇒ 225 - 144 = BC²

⇒ BC² = 81

⇒ BC = $\sqrt{81}$ = 9 m

⇒ AC = AB + BC = 12 + 9 = 21 m.

Hence, Option 3 is the correct option.