Mathematics
A cuboidal block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter that the hemisphere can have ? Also, find the surface area of the solid.
Mensuration
25 Likes
Answer
Cuboidal block of side 7 cm is surmounted by a hemisphere as shown in figure below:
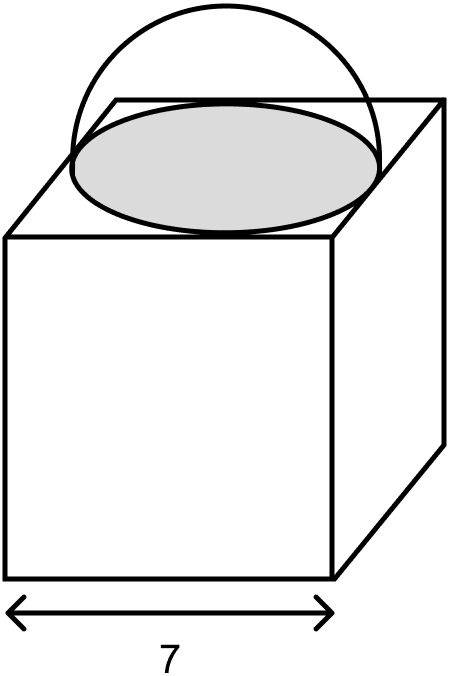
Side of cuboidal block = 7 cm.
Greatest diameter of hemisphere = 7 cm.
Radius =
= = 3.5 cm.
Surface area of the hemisphere = .
Putting values we get,
Surface area of the hemisphere =
Surface area of the cube = 6a2 = 6 x 72 = 6 × 49 = 294 cm2.
Surface area of base of hemisphere = πr2.
Putting values we get,
Surface area of base of hemisphere =
Surface area of solid = Surface area of cube + Surface area of hemisphere - Surface area of base of hemisphere = 294 + 77 - 38.5 = 332.5 cm2.
Hence, the greatest diameter that the hemisphere can have is 7 cm and surface area of the solid is 332.5 cm2.
Answered By
17 Likes
Related Questions
16 glass spheres each of radius 2 cm are packed in a cuboidal box of internal dimensions 16 cm × 8 cm × 8 cm and then the box is filled with water. Find the volume of the water filled in the box.
A cone of maximum volume is carved out of a block of wood of size 20 cm × 10 cm × 10 cm. Find the volume of the remaining wood.
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder (as shown in the adjoining figure). If the height of the cylinder is 10 cm and its base is of radius 3.5 cm, find the total surface area of the article.

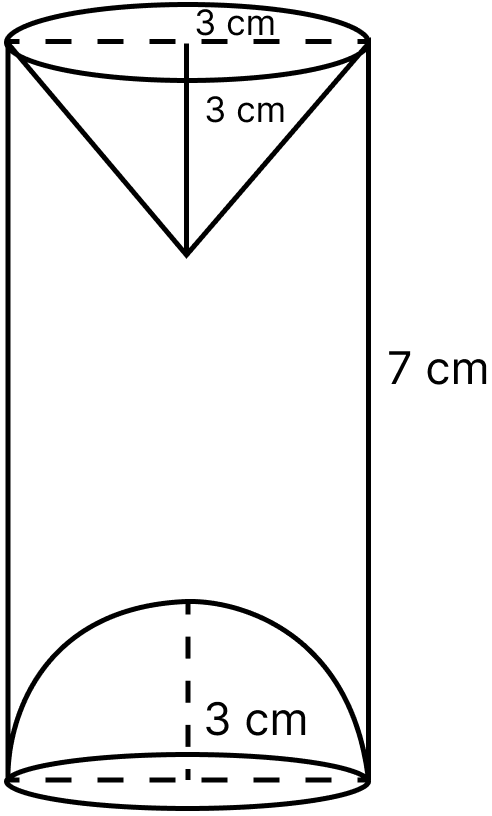
A hemispherical and conical hole are scooped out of a solid wooden cylinder. Find the volume of the remaining solid where the measurements are as follows :
The height of the cylinder is 7 cm, radius of each hemisphere, cone and cylinder is 3 cm. Height of cone is 3 cm. Give your answer correct to nearest whole number. Take π =