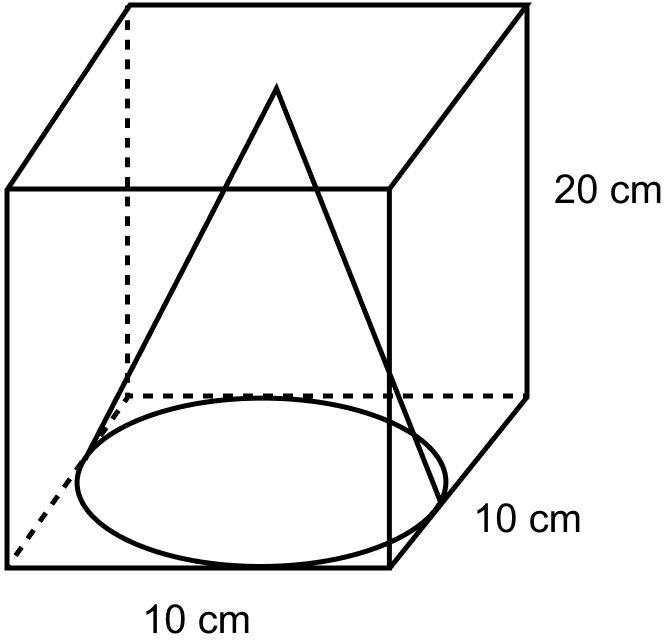
A cone of maximum volume is carved out of a block of wood of size 20 cm × 10 cm × 10 cm. Find the volume of the remaining wood.

Volume of block of wood = 20 cm × 10 cm × 10 cm = 2000 cm³.

Diameter of the cone for maximum volume = 10 cm.

Cone of maximum volume is carved out as shown in figure,

Radius = $\dfrac{\text{Diameter}}{2}$

= $\dfrac{10}{2}$ = 5 cm.

Height of the cone for maximum volume = 20 cm.

Volume of the cone = $\dfrac{1}{3}πr^2h$

Putting values we get,

Volume of cone = $\dfrac{1}{3} \times \dfrac{22}{7} \times 5^2 \times 20$

$= \dfrac{22 \times 25 \times 20}{3 \times 7} \\[1em] = \dfrac{11000}{21} \text{cm}^3.$

Volume of the remaining wood = Volume of block of wood - Volume of the cone.

Volume of remaining wood = $2000 - \dfrac{11000}{21}$

$= \dfrac{(21 \times 2000) - 11000}{21} \\[1em] = \dfrac{42000 - 11000}{21} \\[1em] = \dfrac{31000}{21} \\[1em] = 1476\dfrac{4}{21} \text{ cm}^3.$

Hence, the volume of the remaining wood is $1476\dfrac{4}{21}$ cm³.