Physics
A battery of e.m.f. 16 V and internal resistance 2 Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find (a) the current through the battery (b) p.d. between the terminals of the battery (c) the current in 3 Ω resistor (d) the current in 6 Ω resistor.
Current Electricity
22 Likes
Answer
(a) Given,
e.m.f. = 16 V
internal resistance r = 2 Ω
current through battery = ?
If Rp is the equivalent resistance of resistors 3 Ω and 6 Ω connected in parallel, then
p} = \dfrac{1}{3} + \dfrac{1}{6} \\[0.5em] \dfrac{1}{Rp} = \dfrac{2 + 1}{6} \\[0.5em] \dfrac{1}{Rp} = \dfrac{3}{6} \\[0.5em] \dfrac{1}{Rp} = \dfrac{1}{2} \\[0.5em] \Rightarrow R_p = 2 Ω
From relation,
ε = I (R + r)
Substituting the value in the formula above we get,
16 = I(2 + 2)
⇒ 16 = I x 4 ⇒ I = 16 / 4 = 4 A
Hence, current through the battery = 4 A
(b) Potential difference between the terminals of the battery = ?
Using Ohm's law
V = IR
R = 2 Ω
I = 4 A
Substituting the values in the formula above we get,
V = 4 x 2 = 8 V
Hence, potential difference between the terminals of the battery = 8 V
(c) Current in 3 Ω resistor = ?
Using Ohm's law
V = IR
R = 3 Ω
V = 8 V
I = ?
Substituting the values in the formula above we get,
Hence, current in 3 Ω resistor is 2.66 A
(d) Current in 6 Ω resistor = ?
Using Ohm's law
V = IR
R = 6 Ω
V = 8 V
I = ?
Substituting the values in the formula above we get,
8 = I × 6
⇒ I = 8 / 6 = 1.333 A
Hence, current in 6 Ω resistor is 1.34 A
Answered By
11 Likes
Related Questions
A particular resistance wire has a resistance of 3.0 ohm per meter. Find —
(a) The total resistance of three lengths of this wire each 1.5 m long, joined in parallel.
(b) The potential difference of the battery which gives a current of 2.0 A in each of the 1.5 m length when connected in parallel to the battery (assume that resistance of the battery is negligible).
(c) The resistance of 5 m length of a wire of the same material, but with twice the area of cross section.
A cell supplies a current of 1.2 A through two resistors each of 2 Ω connected in parallel. When the resistors are connected in series, it supplies a current of 0.4 A. Calculate (i) the internal resistance and (ii) e.m.f. of the cell.
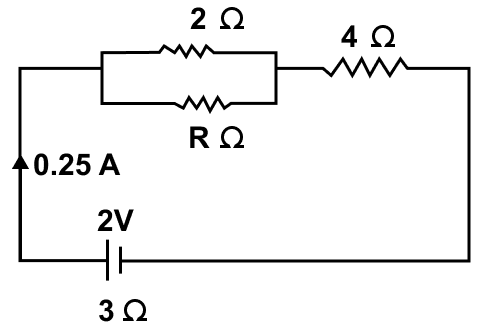
The circuit diagram in figure shows three resistors 2 Ω, 4 Ω and R Ω connected to a battery of e.m.f. 2V and internal resistance 3 Ω. If main current of 0.25 A flows through the circuit, find —
(a) the p.d. across the 4 Ω resistor
(b) the p.d. across the internal resistance of the cell,
(c) the p.d. across the R Ω or 2 Ω resistor, and
(d) the value of R.
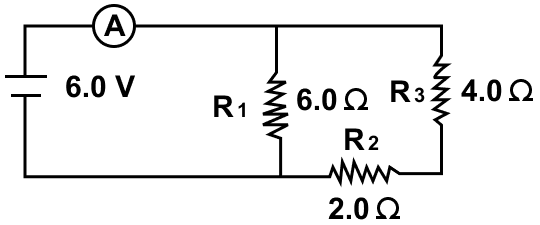
Three resistors of 6.0 Ω, 2.0 Ω and 4.0 Ω are joined to an ammeter A and a cell of e.m.f. 6.0 V as shown in figure. Calculate —
(a) the effective resistance of the circuit, and
(b) the reading of ammeter.